An even simpler, although less accurate, adaptation of Thomson’s setup to measure e/m can be built using a surplus “magic eye” tube. These electron vacuum tubes were commonly used in tube radios as a visual aid for tuning. The purpose of a magic eye tuning tube in these radio receivers was to help tune a station at its strongest point on the dial. The visual aid of the tube made variations in signal strength more obvious than by ear alone.
As shown in Figure 54b, the 6AF6-G tube that we use has a cylindrical cathode heated from its inside by a wire filament. Electrons emitted from the cathode are accelerated horizontally by a high voltage (commonly in the ballpark of 150 V) toward a bowl-shaped anode. As the electrons strike the anode, they cause the phosphor coating on the inside of the bowl to glow. Two “ray-control” electrodes control the size of wedge-shaped shadows produced on the anode’s fluorescent coating. A positive voltage applied to a control electrode reduces its corresponding shadow.
Figure 54 We used a 6AF6-G “magic eye” tuning tube in a simple setup to measure e/m. (a) Circuit diagram of our setup. (b) In the 6AF6, electrons produced by a thermionic cathode cause fluorescence on the tube’s anode. (c) Applying an external magnetic field curves the path of the electrons reaching the anode’s fluorescent coating. Knowing R and the voltage applied to the tube allows one to calculate e/m. (d) We mounted a socket for the tube to a small plastic box, and used banana connectors to make the setup easy to use. The solenoid’s core is a 4-in. section of 2-in. plastic strainer tailpiece pipe.
To measure e/m, we placed a large coil of wire (an air-core solenoid) around the magic eye tube. A current passing through the solenoid subjects the electrons to a vertical magnetic field, deflecting their paths. Without the field, we can assume that the electrons move horizontally at a constant velocity determined by the voltage between the cathode and the anode. When the field is applied, the electrons will be deflected into a circular path, as shown in Figure 54c. We can thus determine e/m if we know the strength of the magnetic field and the radius of the circular path.
The setup is quite simple. We attached a tube socket to a small plastic enclosure, and wired the socket’s contacts to female banana connectors. Next, we cut a 4-in.-long piece off a 2-in.-diameter plastic pipe used in plumbing for sink drains. We used 28AWG enameled magnet wire to wind three layers of turns on the plastic tube. We placed the resulting solenoid on the tube. We wired the tube and solenoid to three power supplies, as shown in Figure 54a. Either one of the high-voltage power supplies that we built (Figure 31 or Figure 32) works well, but one must be very careful not to exceed the 6AF6’s 200-V limit.
Build one yourself and try it out! None of the component values are critical, so feel free to substitute to accommodate what you have in hand. 6AF6-G tubes go for around $20 on eBay. If you don’t have an octal tube socket, or prefer not to solder to one, you may use a relay octal socket base with screw terminals as a very convenient socket for the tube. Oh yeah—make sure you count the exact number of turns that you wind on your solenoid.
We used our Gaussmeter to find that the field produced by our solenoid in the region of the tube’s anode is given by B[Tesla] = 0.0079 × Current[A]. However, as we did before, you could also calculate the magnetic field B inside your solenoid as you energize it with current I if you know the total number of turns in your coil and the length L they occupy:
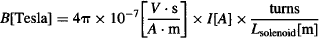
To perform the experiment, dim the lights in the room, turn on the filament, power the tube with 130 V, and wait until it glows. Use a set of cylindrical wooden dowels of known diameters (e.g., 1/4, 1/2, and 3/4 in.), and increase the current through the solenoid until the curve traced by the electrons matches the curve of the dowel. Repeat the measurements at tube voltages V between 90 and 190 V (make sure that you don’t exceed the 6AF6’s 200-V maximum!)
Use your data to estimate the mass of the electron using the formula:
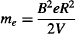
where e = 1.60 × 10−19 Coulomb. How well does your estimate match the accepted value of me = 9.11 × 10−31 kg?
Leave a Reply