In the previous two models for production planning there is a major omission: They do not involve any inventory buildup and depletion. From the familiar EOQ model, we know that there is one possible reason for building inventory, i.e., the presence of fixed ordering cost. A similar reason, which may be more relevant when producing rather than just purchasing items, is the need for a setup time before starting production. Imagine that whenever you want to manufacture red pens you have to carry out a setup of machines, taking three hours. Clearly, your production run cannot just last 20 minutes, as you would waste a lot of production capacity. Modeling fixed charges and setup times calls for binary decision variables, and we will cover such models later in Section 12.4.4.
The EOQ model, by nature, disregards two more possible reasons for building inventories:
- Demand uncertainty, which can be hedged by setting a safety stock level. We have seen a very simple approach in Section 7.8.2. More sophisticated approaches may call for the modeling techniques.
- Demand variability, which is not necessarily due to uncertainty. We have considered seasonality in time series, which is a kind of predictable variability. Now imagine that demand is perfectly known, but features remarkable swings over time. How should we set our capacity level? One possibility is to set a production capacity level corresponding to peak demand, but when demand is low we incur the burden of a lot of expensive resources left unused. Another possibility is setting an intermediate production capacity level, building inventory when demand is low, and depleting inventory when demand is high.
In this section we extend the production mix model in order to account for predictable demand variability; this is our first example of a dynamic decision model. When building a dynamic model, the first issue is whether to represent a continuous or a discrete time. In production planning, discrete time is the standard choice. One good reason is that forecasting models we are familiar with are all based on discrete time buckets. Another reason is that when planning production with, say, weekly time buckets, we build a plan leaving room for lower and more detailed decision levels in charge of executing it. Given this discussion, the first ingredient that we need is a dynamic representation of time and demand. We assume that we have a collection of equal length time buckets, indexed by t = 1, 2, …, T. Let us denote by dit the demand for item i = 1, 2, …, N,18 during time bucket t. In this case, we may allow for a time-varying resource availability Rmt of each resource, indexed by m = 1, …, M. Doing so, we may take into account several practical issues such as time-varying working calendars, holidays, or planned maintenance activities affecting production capacity.
Now what decision variables do we need? Clearly, the production amount is time-varying too, and we may denote by xit the amount of item i produced during time bucket t. Now, we may immediately generalize the capacity constraints we are familiar with:
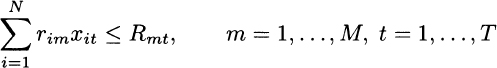
where rim is the amount of resource m required for the production of one unit of item i. Do we need some more decision variables? From the EOQ model, we know that we must account for inventory holding costs. The most natural choice is to introduce a set of decision variables Iit, representing the inventory level of item i, at the end of time bucket t. Please note the difference between variables xit and Iit: We observe inventory levels only at discrete time instants, without checking what happens within each time bucket; hence we assume that Iit refers to the level at the end of each period. By a similar token, we do not know exactly when the amount xit is produced within each time bucket, nor when demand dit is met. We assume that the time bucket is small enough that this is no concern and check inventory balance only at the end of time buckets. Indeed, the inventory balance is a fundamental equation in the model, linking the two sets of decision variables.19 In order to formalize inventory balance, we must carefully specify which objective we are going to pursue – maximization of profit or minimization of cost – as they need not be equivalent.
The case of profit maximization In the static optimal mix model, what we produce and what we sell are the same, since there is no inventory decoupling production and sales. In a dynamic model, we need to specify how much we sell of each item type i during each time bucket t. Let zit be such a variable. Clearly, we cannot sell more than demand, so we should enforce the bound zit ≤ dit. In order to link all of the variables, we need to formalize a rather natural principle: The inventory at the end of time bucket t is the inventory at the beginning of time bucket t, plus what we produced during the time bucket, minus what we sold during the time bucket. Since inventory at the beginning of time bucket t is just inventory at the end of time bucket t − 1, we write
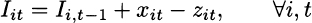
Strictly speaking, we made a little mistake as far as time bucket t = 1 is concerned; for the first time bucket, the constraint involves the initial inventory level Ii0, which is not a decision variable and is part of the problem data. All the involved decision variables are restricted to nonnegative values.
To write the objective function, we need some fundamental economic information concerning each item:
- The inventory holding cost hi
- The unit production cost ci
- The selling price pi where we assume pi > ci
Then, we may write the following LP model:
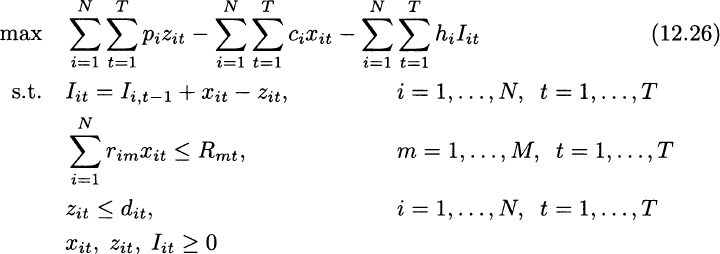
We may make a few observations:
- If the capacity constraints are nonbinding, i.e., if coefficients Rmt are large enough, the optimal solution is obviously
. We satisfy the whole demand producing just in time. It is the capacity constraints that may call for decoupling between production and sales, as well as cause some lost demand. - Even without solving the model, we may be sure that in the optimal solution
, i.e., inventories are depleted during the last time bucket. This happens because, as far as the model is concerned, the world stops at t = T. This kind of “end-of-horizon” effect may induce some distortions, unless T is large enough, and the solution we get is applied according to a “rolling horizon” strategy. The planning horizon rolls forward, in the sense that it initially involves time buckets (1, …, T), then (2, …, T+l), (3, …, T+2), and so on. Only the decision in the first time bucket is actually implemented, as the plan is revised after more information about demand is collected. By doing so, it is reasonable to expect that the end-of-horizon effect will be less critical; however, if the planning horizon is too long, we might lack reliable demand data.
The case of cost minimization If we compare the model above with the EOQ model, we notice a few fundamental differences. Of course, demand is dynamic here, and we might introduce fixed charges or setup costs to make the model more complete and perhaps realistic. But a more fundamental difference is that when we maximize profit we do not take for granted that demand is fully satisfied. On the contrary, in the EOQ model we seek a solution allowing us to meet the whole demand, at minimal cost. In order to build a model more akin to EOQ, we should enforce full satisfaction of demand:
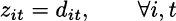
Doing so has a significant impact on the objective function.
- The first term becomes a constant term,
and it may be dropped from the model. Now we are just maximizing a sum of terms multiplied by −1; hence we may transform the maximization into a minimization. - By a similar token, the second term, which is related to production cost, boils down to a constant as well, since what we produce of each item is just the sum of demand over the planning horizon, minus an initial inventory Ii0, plus a possible value IiT, if this is explicitly enforced to avoid the end-of-horizon effect.
So, model (12.26) can be simplified as follows:
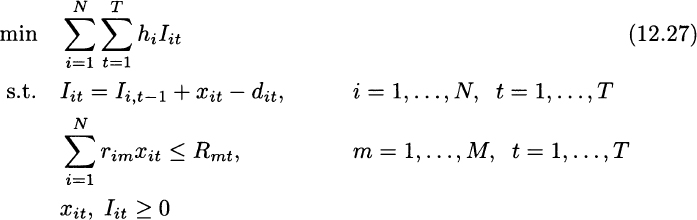
In this model, it is important to emphasize the role of the nonnegativity condition for inventory levels. This, together with inventory balance, implies
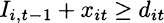
i.e., production during time bucket t plus inventory carried over from the previous time bucket must be enough to cover demand, which is never backlogged. This opens a thorny practical issue: This model, unlike the previous ones, may fail to have a feasible solution. If demand is too large with respect to available capacity, no algorithm will be able to find a solution. This may be rather inconvenient; imagine a production planner sitting in front of a computer informing her that, alas, there is no feasible solution. It would be nice to get some diagnostic clue about which item or which resource seems to be critical and when. Later, in Section 12.3.4, we discuss elastic model formulations that are a possible way to overcome this difficulty.
As a final remark, we may note that, strictly speaking, the introduction of inventory decision variables is not necessary. Assuming full satisfaction of demand, we may substitute inventory holding with the difference between cumulative production and cumulative demand:
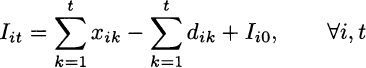
As a general rule, however, model readability should have a higher priority than the reduction of decision variables. Many years ago, when problems had to be solved by hand, such economies were worth pursuing. With lightning-fast hardware doing the work for us now, the amount of decision variables is much less of a concern. Furthermore, state-of-the-art solvers are able to carry out automatic preprocessing of a model, possibly eliminating redundant variables and constraints to improve its solvability, before starting the solution algorithm itself.
Leave a Reply