Almost all wells eventually “feel” their boundaries. In Section 2-2 the steady-state condition implied a constant-pressure outer boundary. Naturally, this boundary can approximate the impact of a larger aquifer. Induced constant pressure may be the result of injector–producer configurations.
For no-flow boundaries, drainage areas can either be described by natural limits such as faults, pinchouts, and so on, or can be artificially induced by the production of adjoining wells.
The pressure at the outer boundary is no longer constant but instead declines at a constant rate with time, as does the pressure at every point in the well drainage volume. That is, ∂p/∂t = constant everywhere. Because the pressure profile is not changing, this condition is often referred to as “pseudosteady state.”
Solving the radial diffusivity equation during pseudosteady state gives the pressure p at any point r in a reservoir of radius re as (Dake, 1978)
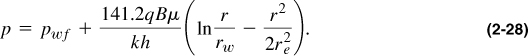
At r = re, Equation (2-28) can be converted to
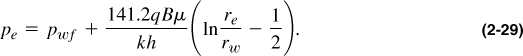
This equation is not particularly useful under pseudosteady state conditions, since pe is not known at any given time. However, as shown in the average reservoir pressure, 
, can be obtained from periodic pressure buildup tests. Therefore, a more useful expression for the pseudosteady state equation would be one using the average reservoir pressure. This is defined as a volumetrically weighted pressure,
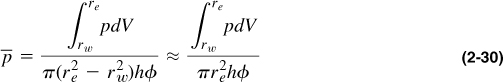
and since dV = 2πrhϕ dr, Equation (2-30) becomes
The expression for the pressure at any point r can be substituted from Equation (2-28), and therefore
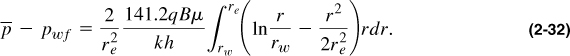
Performing the integration results in
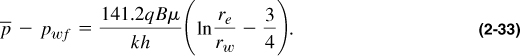
Introducing the skin effect and incorporating the term 3/4 into the logarithmic expression leads to the inflow relationship for a no-flow boundary oil reservoir:
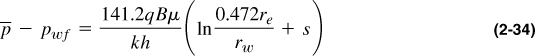
and rearranged for rate
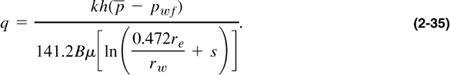
Equation (2-35) is particularly useful because it provides the relationship between the average reservoir pressure, , and the rate q. The average pressure, , is a variable that can be determined from a pressure buildup test. It depends on the drainage area and the properties of the fluid and rock. Material balance calculations presented combine depletion mechanisms with inflow relationships and lead to forecasts of well performance and cumulative production.
Finally, while Equation (2-35) appears similar to Equation (2-9) (for steady-state flow), the two should never be confused. They represent distinctly different reservoir production mechanisms. However, both lead to similar expressions for the dimensionless productivity index, JD. For steady state:
and for pseudosteady state:
In both cases, for typical drainage and well radii, the logarithmic term ranges between 7 and 9, and thus for an undamaged or unstimulated well the JD is of the order of 0.1; smaller values denote damage, and larger values denote stimulation, hydraulic fracturing, or more favorable well geometry such as horizontal or multilateral wells.
Example 2-4. Production from a No-Flow Boundary Reservoir
What would be the average reservoir pressure if the outer boundary pressure is 6000 psi, the flowing bottomhole pressure is 3000 psi, the drainage area is 640 acres, and the well radius is 0.328 ft? What would be the ratio of the flow rates before (q1) and after (q2) the average reservoir pressure drops by 1000 psi? Assume that s = 0.
Solution
A ratio of Equations (2-29) and (2-33) results in
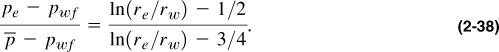
The drainage area A = 640 and therefore re = 2980 ft. Substituting the given variables in Equation (2-38) results in
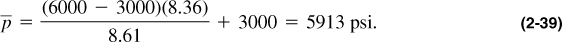
The flow-rate ratio after the 1000 psi average pressure decline would be
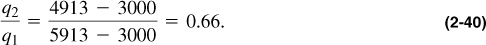
Leave a Reply