Once the pressure disturbance has been felt throughout the reservoir including at the boundary, the reservoir can no longer be considered as being infinite in size and the flow is not in the transient regime. This situation necessitates another solution to Eq. (8.38), using a different boundary condition at the outer boundary. The initial condition remains the same as before (i.e., the reservoir pressure is pi throughout the reservoir at time t = 0). The flow rate is again treated as constant at the wellbore. The new boundary condition used to find a solution to the radial diffusivity equation is that the outer boundary of the reservoir is a no-flow boundary. In mathematical terms,
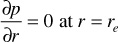
Applying these conditions to Eq. (8.38), the solution for the pressure at the wellbore becomes
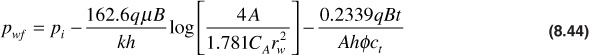
where A is the drainage area of the well in square feet and CA is a reservoir shape factor. Values of the shape factor are given in Table 8.2 for several reservoir types. Equation (8.44) is valid only for sufficiently long enough times for the flow to have reached the pseudosteady-state time period.
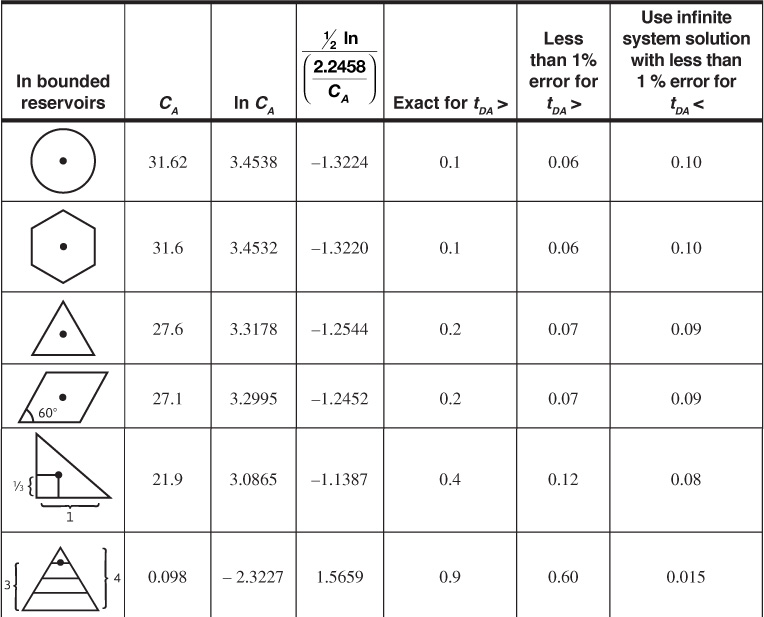
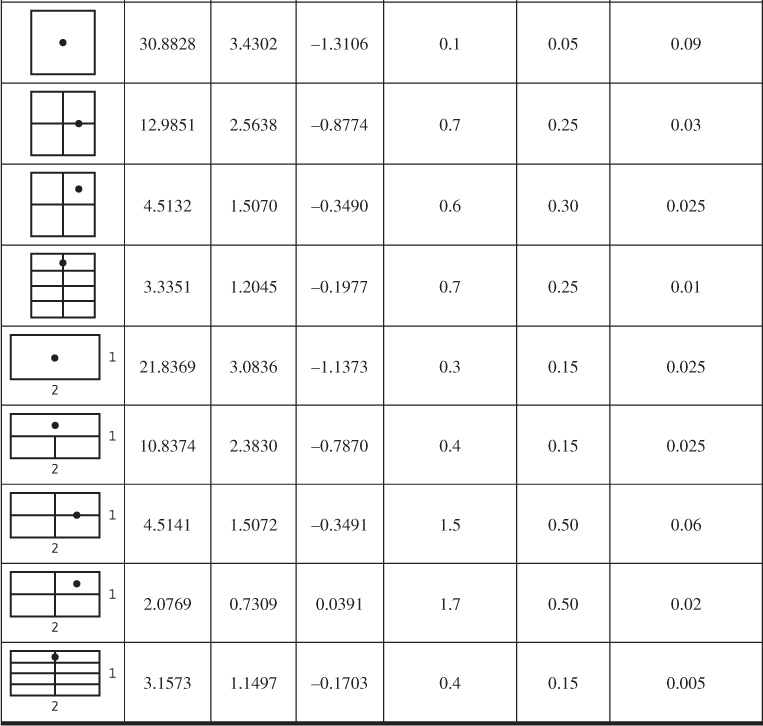
Table 8.2 Shape Factors for Various Single-Well Drainage Areas (after Earlougher3)
After reaching pseudosteady-state flow, the pressure at every point in the reservoir is changing at the same rate, which suggests that the average reservoir pressure is also changing at the same rate. The volumetric average reservoir pressure, which is usually designated as ![]() and is the pressure used to calculate fluid properties in material balance equations, is defined as
and is the pressure used to calculate fluid properties in material balance equations, is defined as

where pj is the average pressure in the jth drainage volume and Vj is the volume of the jth drainage volume. It is useful to rewrite Eq. (8.44) in terms of the average reservoir pressure, ![]() :
:
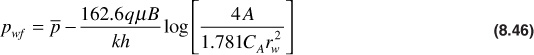
For a well in the center of a circular reservoir with a distance to the outer boundary of re, Eq. (8.46) reduces to
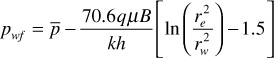
If this equation is rearranged and solved for q,
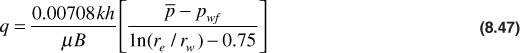
Leave a Reply