Radial Flow of Compressible Fluids, Transient Flow

Eq. (8.35)

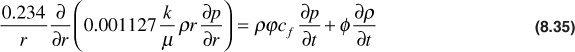
was developed to describe the flow of any fluid flowing in a radial geometry in porous media. To develop a solution to Eq. (8.35) for the compressible fluid, or gas, case, two additional equations are required: (1) an equation of state, usually the real gas law, which is Eq. (2.8), and (2) Eq. (2.18), which describes how the gas isothermal compressibility varies with pressure:

These three equations can be combined to yield

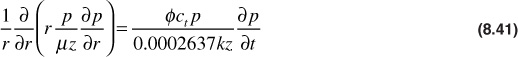
Applying the real gas pseudopressure transformation to Eq. (8.41) yields the following:

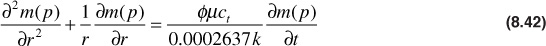
Equation (8.42) is the diffusivity equation for compressible fluids, and it has a very similar form to Eq. (8.38), which is the diffusivity equation for slightly compressible fluids. The only difference in the appearance of the two equations is that Eq. (8.42) has the real gas pseudopressure, m(p), substituted for p. There is another significant difference that is not apparent from looking at the two equations. This difference is in the assumption concerning the magnitude of the (∂p/∂r)² term in Eq. (8.41). To linearize Eq. (8.41), it is necessary to limit the term to a small value so that it results in a negligible quantity, which is normally the case for liquid flow applications. This limitation is not necessary for the gas equation. Since pressure gradients around the gas wells can be very large, the transformation of variables has led to a much more practical and useful equation for gases.

Equation (8.42) is still a nonlinear differential equation because of the dependence of μ and c_t on pressure or the real gas pseudopressure. Thus, there is no analytical solution for Eq. (8.42). Al-Hussainy and Ramey, however, used finite difference techniques to obtain an approximate solution to Eq. (8.42).¹¹ The result of their studies for pressures at the wellbore (i.e., where the logarithm approximation to the E_i function can be made) is the following equation:

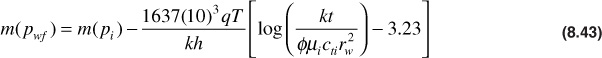
where p_wf is the flowing pressure at the wellbore; p_i is the initial reservoir pressure; q is the flow rate in SCF/day at standard conditions of 60°F and 14.7 psia; T is the reservoir temperature in °R; k is in md; h is in ft; t is in hr; μ_i is in cp and is evaluated at the initial pressure, p_i, c_ti is in psi^–1 and is also evaluated at p_i; and r_w is the wellbore radius in feet. Equation (8.43) can be used to calculate the flowing pressure at the sandface of a gas well.