Permeability Averages for Radial Flow

Many producing formations are composed of strata or stringers that may vary widely in permeability and thickness, as illustrated in Fig. 8.10. If these strata are producing fluid to a common wellbore under the same drawdown and from the same drainage radius, then

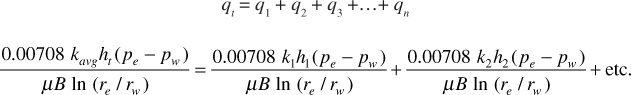
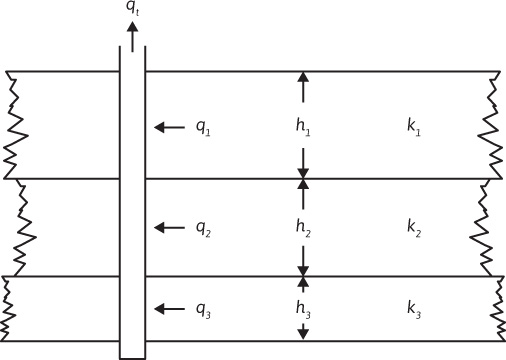
Figure 8.10 Radial flow in parallel beds.

Then, canceling,

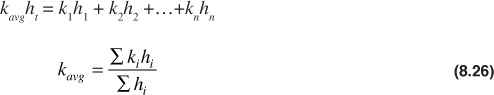
This equation is the same as for parallel flow in linear beds with the same bed width. Here, again, average permeability refers to that permeability by which all beds could be replaced and still obtain the same production rate under the same drawdown. The product kh is called the flow capacity or transmissivity of a bed or stratum, and the total flow capacity of the producing formation, ∑k_ih_i, is usually expressed in millidarcy-feet. Because the rate of flow is directly proportional to the flow capacity, Eq. (8.21), a 10-ft bed of 100 md will have the same production rate as a 100-ft bed of 10-md permeability, other things being equal. There are limits of formation flow capacity below which production rates are not economic, just as there are limits of net productive formation thicknesses below which wells will never pay out. Of two formations with the same flow capacity, the one with the lower oil viscosity may be economic but the other may not, and the available pressure drawdown enters in similarly. Net sand thicknesses of the order of 5 ft and capacities of the order of a few hundred millidarcy-feet are likely to be uneconomic, depending on other factors such as available drawdown, viscosity, porosity, connate water, depth, and the like, or will require hydraulic fracture stimulation. The flow capacity of the formation together with the viscosity also determines to a large extent whether a well will flow or whether artificial lift must be used. The amount of solution gas is an important factor. With hydraulic fracturing (to be discussed later), the well productivity in low flow capacity reservoirs can be greatly improved.

We now consider a radial flow system of constant thickness with a permeability of k_e between the drainage radius r_e and some lesser radius r_a and an altered permeability k_a between the radius r_a and the wellbore radius r_w, as shown in Fig. 8.11. The pressure drops are additive, and

(p_e – p_w) = (p_e – p_a) + (p_a – p_w)

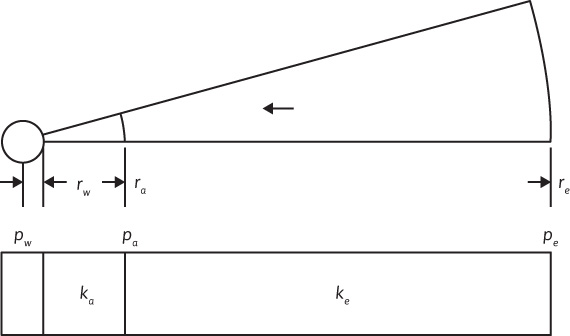
Figure 8.11 Radial flow in beds in series.

Then, from Eq. (8.21),

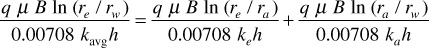
Canceling and solving for k_avg,

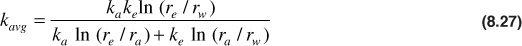
Equation (8.27) may be extended to include three or more zones in series. This equation is important in studying the effect of a decrease or increase of permeability in the zone about the wellbore on the well productivity.