In 1856, as a result of experimental studies on the flow of water through unconsolidated sand filter beds, Henry Darcy formulated the law that bears his name. This law has been extended to describe, with some limitations, the movement of other fluids, including two or more immiscible fluids, in consolidated rocks and other porous media. Darcy’s law states that the velocity of a homogeneous fluid in a porous medium is proportional to the driving force and inversely proportional to the fluid viscosity, or
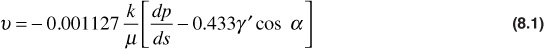
where
ν = the apparent velocity, bbl/day-ft2
k = permeability, millidarcies (md)
μ = fluid viscosity, cp
p = pressure, psia
s = distance along flow path in ft
γ′ = fluid specific gravity (always relative to water)
α = the angle measured counterclockwise from the downward vertical to the positive s direction
and the term
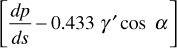
represents the driving force. The driving force may be caused by fluid pressure gradients (dp/ds) and/or hydraulic (gravitational) gradients (0.433γ′ cos α). In many cases of practical interest, the hydraulic gradients, although always present, are small compared with the fluid pressure gradients and are frequently neglected. In other cases, notably production by pumping from reservoirs whose pressures have been depleted and gas-cap expansion reservoirs with good gravity drainage characteristics, the hydraulic gradients are important and must be considered.
The apparent velocity, ν, is equal to qB/A, where q is the volumetric flow rate in STB/day, B is the formation volume factor, and A is the apparent or total area of the bulk rock material in square feet perpendicular to the flow direction. A includes the area of the solid rock material as well as the area of the pore channels. The fluid pressure gradient, dp/ds, is taken in the same direction as ν and q. The negative sign in front of the constant 0.001127 indicates that if the flow is taken as positive in the positive s-direction, then the pressure decreases in that direction, so the slope dp/ds is negative.
Darcy’s law applies only in the region of laminar flow characterized by low fluid velocities; in turbulent flow, which occurs at high fluid velocities, the pressure gradient is dependent on the flow rate but usually increases at a greater rate than does the flow rate. Fortunately, Darcy’s law is valid for liquid flow, except for some instances of quite large production or injection rates in the vicinity of the wellbore, the flow in the reservoir, and most laboratory tests. However, gas flowing near the wellbore is likely to be subject to non-Darcy flow. Darcy’s law does not apply to flow within individual pore channels but to portions of a rock, the dimensions of which are reasonably large compared with the size of the pore channels. In other words, it is a statistical law that averages the behavior of many pore channels. For this reason, although samples with dimensions of a centimeter or two are satisfactory for permeability measurements on uniform sandstones, much larger samples are required for reliable measurements of fracture and vugular-type rocks.
Owing to the porosity of the rock, the tortuosity of the flow paths, and the absence of flow in some of the (dead) pore spaces, the actual fluid velocity within pore channels varies from point to point within the rock and maintains an average that is many times the apparent bulk velocity. Because actual velocities are in general not measurable, and to keep porosity and permeability separated, apparent velocity forms the basis of Darcy’s law. This means the actual average forward velocity of a fluid is the apparent velocity divided by the porosity where the fluid completely saturates the rock.
A basic unit of permeability is the darcy (d). A rock of 1-d permeability is one in which a fluid of 1-cp viscosity will move at a velocity of 1 cm/sec under a pressure gradient of 1 atm/cm. Since this is a fairly large unit for most producing rocks, permeability is commonly expressed in units one thousandth as large, the millidarcy, or 0.001 d. Throughout this text, the unit of permeability used is the millidarcy (md). Conventional oil and gas sands have permeabilities varying from a few millidarcies to several thousands. Intergranular limestone permeabilities may be only a fraction of a millidarcy and yet be commercial if the rock contains additional natural or artificial fractures or other kinds of openings. Fractured and vugular rocks may have enormous permeabilities, and some cavernous limestones approach the equivalent of underground tanks. In recent years, unconventional reservoirs have been developed with permeabilities in the microdarcy (1μd = 10–6 d) or even nanodarcy (1 nd = 10–9 d) range.
The permeability of a sample as measured in the laboratory may vary considerably from the average of the reservoir as a whole or a portion thereof. There are often wide variations both laterally and vertically, with the permeability sometimes changing several fold within an inch in rock that appears quite uniform. Generally, the permeability measured parallel to the bedding planes of stratified rocks is larger than the vertical permeability. Also, in some cases, the permeability along the bedding plane varies considerably and consistently with core orientation, owing presumably to the oriented deposition of more or less elongated particles and/or the subsequent leaching or cementing action of migrating waters. Some reservoirs show general permeability trends from one portion to another, and many reservoirs are closed on all or part of their boundaries by rock of very low permeability, certainly by the overlying caprock. The occurrence of one or more strata of consistent permeability over a portion or all of a reservoir is common. In the proper development of reservoirs, it is customary to core selected wells throughout the productive area measuring the permeability and porosity on each foot of core recovered. The results are frequently handled statistically.1,2 In very heterogeneous reservoirs, especially carbonates, it may be that no core is retrieved from the most productive intervals because they are highly fractured or even rubblized. For such reservoirs core-derived permeability statistics may be very conservative or even misleadingly low.
Hydraulic gradients in reservoirs vary from a maximum near 0.500 psi/ft for brines to 0.433 psi/ft for fresh water at 60°F, depending on the pressure, temperature, and salinity of the water. Reservoir oils and high-pressure gas and gas-condensate gradients lie in the range of 0.10–0.30 psi/ft, depending on the temperature, pressure, and composition of the fluid. Gases at low pressure will have very low gradients (e.g., about 0.002 psi/ft for natural gas at 100 psia). The figures given are the vertical gradients. The effective gradient is reduced by the factor cos α. Thus a reservoir oil with a reservoir specific gravity of 0.60 will have a vertical gradient of 0.260 psi/ft; however, if the fluid is constrained to flow along the bedding plane of its stratum, which dips at 15° (α = 75°), then the effective hydraulic gradient is only 0.26 cos 75°, or 0.067 psi/ft. Although these hydraulic gradients are small compared with usual reservoir pressures, the fluid pressure gradients, except in the vicinity of wellbores, are also quite small and in the same range. Fluid pressure gradients within a few feet of wellbores may be as high as tens of psi per foot due to the flow into the wellbore but will fall off rapidly away from the well, inversely with the radius.
Frequently, static pressures measured from well tests are corrected to the top of the production (perforated) interval with a knowledge of the reservoir fluid gradient. They also can be adjusted to a common datum level for a given reservoir by using the same reservoir fluid gradient. Example 8.1 shows the calculation of apparent velocity by two methods. The first is by correcting the well pressures to the datum level using information about hydraulic gradients. The second is by using Eq. (8.1).
Example 8.1 Calculating Datum Level Pressures, Pressure Gradients, and Reservoir Flow from Static Pressure Measurements in Wells
Given
Distance between wells (see Fig. 8.1)
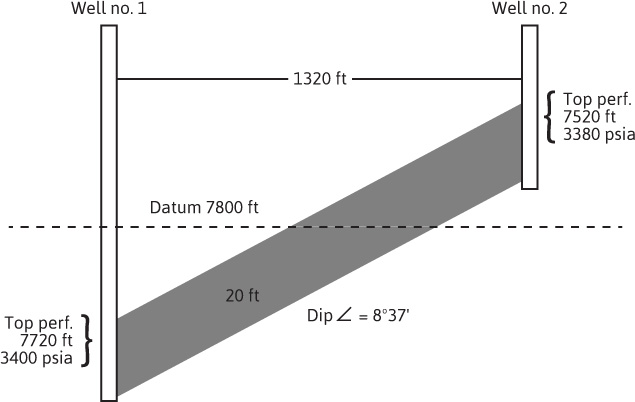
Figure 8.1 Cross section between the two wells of Example 8.1. Note exaggerated vertical scale.
True stratum thickness = 20 ft
Dip of stratum between wells = 8° 37′
Reservoir datum level = 7600 ft subsea
Reservoir fluid specific gravity = 0.693 (water = 1.00)
Reservoir permeability = 145 md
Reservoir fluid viscosity = 0.32 cp
Well number 1 static pressure = 3400 psia at 7720 ft subsea
Well number 2 static pressure = 3380 psia at 7520 ft subsea
First Solution
Reservoir fluid gradient = Reservoir fluid specific gravity × Hydraulic gradient fresh water = 0.693 × 0.433 = 0.300 psi/ft
p1 at 7600 ft datum = Well number 1 static pressure – (Elevation difference of well number 1 and datum × Reservoir fluid gradient) = 3400 – 120 × 0.30 = 3364 psia
p2 at 7600 ft datum = Well number 2 static pressure + (Elevation difference of well number 2 and datum × Reservoir fluid gradient) = 3380 + 80 × 0.30 = 3404 psia
The difference of 40 psi indicates that fluid is moving downdip, from well 2 to well 1. The average effective gradient is 40/1335 = 0.030 psi/ft, where 1335 is the distance along the stratum between the wells. The velocity then is
v = 0.001127 × (Reservoir permeability / Reservoir fluid viscosity) × Average effective gradient
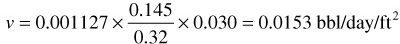
Second Solution
Take the positive direction from well 1 to well 2. Then α = 98° 37′ and cos α = –0.1458.
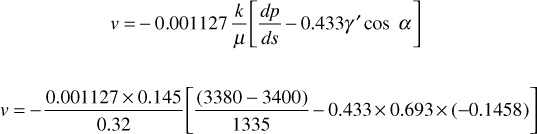
v = –0.0153 bbl/day/sq ft
The negative sign indicates that fluid is flowing in the negative direction (i.e., from well 2 to well 1).
Equation (8.1) suggests that the velocity and pressure gradient are related by the mobility. The mobility, given the symbol λ, is the ratio of permeability to viscosity, k/μ. The mobility appears in all equations describing the flow of single-phase fluids in reservoir rocks. When two fluids are flowing simultaneously—for example, gas and oil to a wellbore, it is the ratio of the mobility of the gas, λg, to that of the oil, λo, that determines their individual flow rates. The mobility ratio M is an important factor affecting the displacement efficiency of oil by water. When one fluid displaces another, the standard notation for the mobility ratio is the mobility of the displacing fluid to that of the displaced fluid. For water-displacing oil, it is λw/λo.
Leave a Reply