The precision of the reserve calculations by the volumetric method depends on the accuracy of the data that enter the computations. The precision of the initial gas in place depends on the probable errors in the averages of the porosity, connate water, pressure, and gas deviation factor and in the error in the determination of the bulk productive volume. With the best of core and log data in rather uniform reservoirs, it is doubtful that the initial gas in place can be calculated more accurately than about 5%, and the figure will range upward to 100% or higher, depending on the uniformity of the reservoir and the quantity and quality of the data available.
The reserve is the product of the gas in place and the recovery factor. For volumetric reservoirs, the reserve of the reservoir as a whole, for any selected abandonment pressure, should be known to about the same precision as the initial gas in place. Water-drive reservoirs require, in addition, the estimate of the volume of the reservoir invaded at abandonment and the average residual gas saturation. When the reservoir exhibits permeability stratification, the difficulties are increased and the accuracy is therefore reduced. In general, reserve calculations are more accurate for volumetric than for water-drive reservoirs. When the reserves are placed on a well or lease basis, the accuracy may be reduced further because of lease drainage, which occurs in both volumetric and water-drive reservoirs.
The use of the material balance equation to calculate gas in place involves the terms of the gas volume factor. The precision of the calculations is, of course, a function of the probable error in these terms. The error in gas production Gp arises from error in gas metering, in the estimate of lease use and leakage, and in the estimate of the low-pressure separator or stock-tank gases. Sometimes underground leakage occurs—from the failure in casing cementing, from casing corrosion, or, in the case of dual completions, from leakage between the two zones. When gas is commingled from two reservoirs at the surface prior to metering, the division of the total between the two reservoirs depends on periodic well tests, which may introduce additional inaccuracies. Meters are usually calibrated to an accuracy of 1%, and, therefore, it is doubtful that the gas production under the best of circumstances is known closer than 2%. Average accuracies are in the range of a few to several percentage points.
Pressure errors are a result of gauge errors and the difficulties in averaging, particularly when there are large pressure differences throughout the reservoir. When reservoir pressures are estimated from measured wellhead pressures, the errors of this technique enter the calculations. When the field is not fully developed, the average pressure is, of course, taken from the developed portion, which is lower than that of the reservoir as a whole. Water production with gas wells is frequently unreported when the amount is small; when it is appreciable, it is often estimated from periodic well tests.
Under the best of circumstances, the material balance estimates of the gas in place are seldom more accurate than 5% and may range much higher. The estimate of reserves is, of course, one step removed.
Problems
4.1 A volumetric gas field has an initial pressure of 4200 psia, a porosity of 17.2%, and connate water of 23%. The gas volume factor at 4200 psia is 0.003425 ft3/SCF and at 750 psia is 0.01852 ft3/SCF.
(a) Calculate the initial in-place gas in standard cubic feet on a unit basis.
(b) Calculate the initial gas reserve in standard cubic feet on a unit basis, assuming an abandonment pressure of 750 psia.
(c) Explain why the calculated initial reserve depends on the abandonment pressure selected.
(d) Calculate the initial reserve of a 640-acre unit whose average net productive formation thickness is 34 ft, assuming an abandonment pressure of 750 psia.
(e) Calculate the recovery factor based on an abandonment pressure of 750 psia.
4.2 Discovery well 1 and wells 2 and 4 produce gas in the 7500-ft reservoir of the Echo Lake Field (Fig. 4.8). Wells 3 and 7 were dry in the 7500-ft reservoir; however, together with their electric logs and the one from well 1, the fault that seals the northeast side of the reservoir was established. The logs of wells 1, 2, 4, 5, and 6 were used to construct the map of Fig. 4.8, which was used to locate the gas-water contact and determine the average net sand thickness. The reservoir had been producing for 18 months when well 6 was drilled at the gas-water contact. The static wellhead pressures of the production wells showed virtually no decline during the 18-month period before drilling well 6 and averaged near 3400 psia. The following data were available from electric logs, core analysis, and the like:
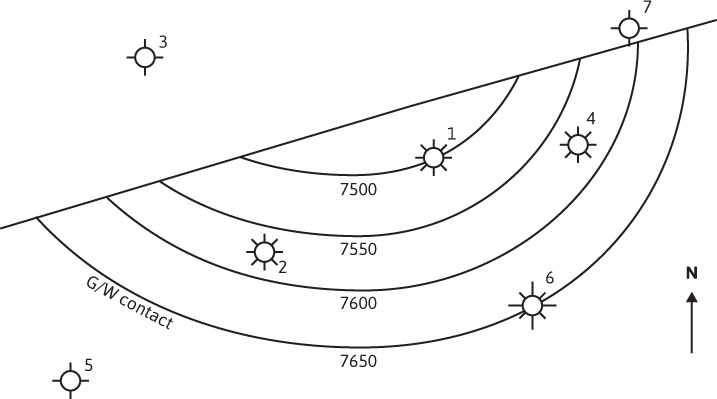
Figure 4.8 Echo Lake Field, subsurface map, 7500-ft reservoir.
Average well depth = 7500 ft
Average static wellhead pressure = 3400 psia
Reservoir temperature = 175°F
Gas specific gravity = 0.700
Average porosity = 27%
Average connate water = 22%
Standard conditions = 14.7 psia and 60°F
Bulk volume of productive reservoir rock at the time well 6 was drilled = 22,500 ac-ft
(a) Calculate the reservoir pressure.
(b) Estimate the gas deviation factor and the gas volume factor.
(c) Calculate the reserve at the time well 6 was drilled, assuming a residual gas saturation of 30%.
(d) Discuss the location of well 1 with regard to the overall gas recovery.
(e) Discuss the effect of sand uniformity on overall recovery—for example, a uniform permeable sand versus a sand in two beds of equal thickness, with respective permeabilities of 500 md and 100 md.
4.3 The M Sand is a small gas reservoir with an initial bottom-hole pressure of 3200 psia and bottom-hole temperature of 220°F. It is desired to inventory the gas in place at three production intervals. The pressure-production history and gas volume factors are as follows:
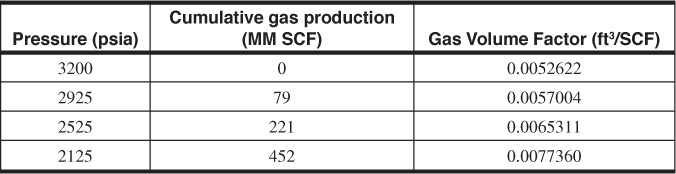
(a) Calculate the initial gas in place using production data at the end of each of the production intervals, assuming volumetric behavior.
(b) Explain why the calculations of part (a) indicate a water drive.
(c) Show that a water drive exists by plotting the cumulative production versus p/z.
(d) Based on electric log and core data, volumetric calculations on the M Sand showed that the initial volume of gas in place is 1018 MM SCF. If the sand is under a partial water drive, what is the volume of water encroached at the end of each of the periods? There was no appreciable water production.
4.4 When the Sabine Gas Field was brought in, it had a reservoir pressure of 1700 psia and a temperature of 160°F. After 5.00 MMM SCF was produced, the pressure fell to 1550 psia. If the reservoir is assumed to be under volumetric control, using the deviation factors of Problem 2.10, calculate the following:
(a) The hydrocarbon pore volume of the reservoir.
(b) The SCF produced when the pressure falls to 1550, 1400, 1100, 500, and 200 psia. Plot cumulative recovery in SCF versus p/z.
(c) The SCF of gas initially in place.
(d) From your graph, find how much gas can be obtained without the use of compressors for delivery into a pipeline operating at 750 psia.
(e) What is the approximate pressure drop per MMM SCF of production?
(f) Calculate the minimum value of the initial reserve if the produced gas measurement is accurate to ±5% and if the average pressures are accurate to ±12 psi when 5.00 MMM SCF have been produced and the reservoir pressure has dropped to 1550 psia.
4.5 If, however, during the production of 5.00 MMM SCF of gas in the preceding problem, 4.00 MM bbl of water encroaches into the reservoir and still the pressure has dropped to 1550 psia, calculate the initial in-place gas. How does this compare with Problem 4.4(c)?
4.6 (a) The gas cap of the St. John Oil Field had a bulk volume of 17,000 ac-ft when the reservoir pressure had declined to 634 psig. Core analysis shows an average porosity of 18% and an average interstitial water of 24%. It is desired to increase the recovery of oil from the field by repressuring the gas cap to 1100 psig. Assuming that no additional gas dissolves in the oil during repressuring, calculate the SCF required. The deviation factors for both the reservoir gas and the injected gas are 0.86 at 634 psig and 0.78 at 1100 psig, both at 130°F.
(b) If the injected gas has a deviation factor of 0.94 at 634 psig and 0.88 at 1100 psig and the reservoir gas deviation factors match those presented in (a), recalculate the injected gas required.
(c) Is the assumption that no additional solution gas will enter the reservoir oil a valid one?
(d) Considering the possibility of some additional solution gas and the production of oil during the time of injection, will the figure of part (a) be maximum or minimum? Explain.
(e) Explain why the gas deviation factors are higher (closer to unity) for the injected gas in part (b) than for the reservoir gas.
4.7 The following production data are available from a gas reservoir produced under volumetric control:

The initial reservoir temperature was 237°F, and the reservoir gas gravity is 0.7.
(a) What will be the cumulative gas production at 2500 psia?
(b) What fraction of the initial reservoir gas will be produced at 2500 psia?
(c) What was the initial reservoir pressure?
4.8 (a) A well drilled into a gas cap for gas recycling purposes is found to be in an isolated fault block. After 50 MM SCF was injected, the pressure increased from 2500 to 3500 psia. Deviation factors for the gas are 0.90 at 3500 and 0.80 at 2500 psia, and the bottom-hole temperature is 160°F. How many cubic feet of gas storage space are in the fault block?
(b) If the average porosity is 16%, average connate water is 24%, and average sand thickness is 12 ft, what is the areal extent of the fault block?
4.9 The initial volume of gas in place in the P Sand reservoir of the Holden Field is calculated from electric log and core data to be 200 MMM SCF underlying 2250 productive acres, at an initial pressure of 3500 psia and 140°F. The pressure-production history is

(a) What is the initial volume of gas in place as calculated from the pressure-production history, assuming no water influx?
(b) Assuming uniform sand thickness, porosity, and connate water, if the volume of gas in place from pressure-production data is believed to be correct, how many acres of extension to the present limits of the P Sand are predicted?
(c) If, on the other hand, the gas in place calculated from the log and core data is believed to be correct, how much water influx must have occurred during the 75 MMM SCF of production to make the two figures agree?
4.10 Explain why initial calculations of gas in place are likely to be in greater error during the early life of depletion reservoirs. Will these factors make the predictions high or low? Explain.
4.11 A gas reservoir under partial water drive produced 12.0 MMM SCF when the average reservoir pressure dropped from 3000 psia to 2200 psia. During the same interval, an estimated 5.20 MM bbl of water entered the reservoir based on the volume of the invaded area. If the gas deviation factor at 3000 psia and bottom-hole temperature of 170°F is 0.88 and at 2200 psia is 0.78, what is the initial volume of gas in place measured at 14.7 psia and 60°F?
4.12 A gas-producing formation has uniform thickness of 32 ft, a porosity of 19%, and connate water saturation of 26%. The gas deviation factor is 0.83 at the initial reservoir pressure of 4450 psia and reservoir temperature of 175°F.
(a) Calculate the initial in-place gas per acre-foot of bulk reservoir rock.
(b) How many years will it take a well to deplete by 50% a 640-acre unit at the rate of 3 MM SCF/day?
(c) If the reservoir is under an active water drive so that the decline in reservoir pressure is negligible and, during the production of 50.4 MMM SCF of gas, water invades 1280 acres, what is the percentage of recovery by water drive?
(d) What is the gas saturation as a percentage of total pore space in the portion of the reservoir invaded by water?
4.13 Fifty billion standard cubic feet of gas has been produced from a dry gas reservoir since its discovery. The reservoir pressure during this production has dropped to 3600 psia. Your company, which operates the field, has contracted to use the reservoir as a gas storage reservoir. A gas with a gravity of 0.75 is to be injected until the average pressure reaches 4800 psia. Assume that the reservoir behaves volumetrically, and determine the amount of SCF of gas that must be injected to raise the reservoir pressure from 3600 to 4800 psia. The initial pressure and temperature of the reservoir were 6200 psia and 280°F, respectively, and the specific gravity of the reservoir gas is 0.75.
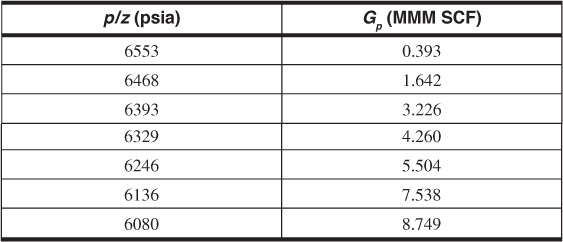
4.14 The production data for a gas field are given in the following table. Assume volumetric behavior and calculate the following:
(a) Determine the initial gas in place.
(b) What percentage of the initial gas in place will be recovered at p/z of 1000?
(c) The field is to be used as a gas storage reservoir into which gas is injected during summer months and produced during the peak demand months of the winter. What is the minimum p/z value that the reservoir needs to be brought back up to if a supply of 50 MMM SCF of gas is required and the abandonment p/z is 1000?
4.15 Calculate the daily gas production, including the condensate and water gas equivalents, for a reservoir with the following daily production:
Separator gas production = 6 MM SCF
Condensate production = 100 STB
Stock-tank gas production = 21 M SCF
Freshwater production = 10 surface bbl
Initial reservoir pressure = 6000 psia
Current reservoir pressure = 2000 psia
Reservoir temperature = 225°F
Water vapor content of 6000 psia and 225°F = 0.86 bbl/MM SCF
Condensate gravity = 50 °API
Leave a Reply