At 0°C
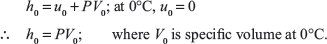
0°C to Saturation Temperature

For Complete Transformation of Steam
hfg = hg – hf = (ug – uf) + P (Vg – Vf) kJ/kg
Wet Steam
Wet steam contains partly water as suspended in it and partly steam.
Dryness Fraction
Dryness fraction is defined as the mass of dry steam per kg of wet steam. It is represented by x.
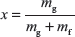
Enthalpy
h = xhg + (1 – x) hf = hf + xhfg
Specific Volume
V = xVg + (1 – x) Vf = Vf + xVfg
Internal Energy
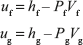
Entropy of Water
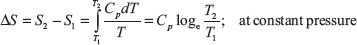
Entropy of Steam
![]() for dry saturated steam at constant pressure (x = 1)
for dry saturated steam at constant pressure (x = 1)
![]() for wet steam at constant pressure
for wet steam at constant pressure
![]() for superheated steam at constant pressure
for superheated steam at constant pressure
where Cpw ≈ 1, specific heat of water.
Since value of Cp varies, the values of entropy from these equations are not accurate; this can be taken from steam table.
Example 4.1: (i) Find the temperature, enthalpy, entropy, internal energy, specific volume of 1 kg of dry saturated steam at 10 bar.
(ii) What are the changes in these properties from saturated liquid to dry saturated vapour at the same pressure.
- From steam table, properties of dry saturated steam at 10 bar or 1 MPa are given below:Temperature, t = 179.91°C

-

Example 4.2: A 2 m3 drum is to be completely filled with a saturated steam at 10 bar. First, the drum is evacuated then the necessary amount of water is filled and evaporated by heating.
- What mass of water is required and what will be temperature of the vapour?
- If the drum finally contains a two-phase system with dryness fraction of 90%. What will be the required mass?
Solution:
From steam table:
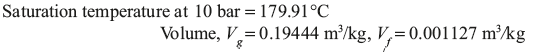
Example 4.3: A container of volume 0.05 m3 contains a mixture of saturated water and saturated steam at temperature 300°C. The mass of water is 10 kg. Find the pressure, mass, specific volume, enthalpy, entropy, and internal energy.
Solution:
From temperature based saturated steam
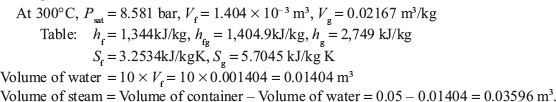
Mass of steam = Volume of steam/Specific volume of steam = 0.03596/0.02167 = 1.659 kg.
Total mass of mixture = Mass of water + Mass of steam = 10 + 1.659 = 11.659 kg.
Quality of steam, X = Mass of steam/(Mass of water + Mass of steam) = 1.659/11.659 = 0.1422
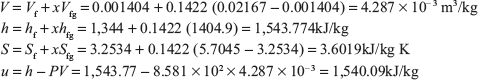
Example 4.4: Steam at 1 MPa, 300°C and flowing at the rate of 1 kg/s passes into a pipe carrying wet steam at 1 MPa and 0.8 dryness fraction. After adiabatic mixing, the flow rate becomes 2.5 kg/s as shown in Figure 4.4. Determine the condition of steam after mixing.
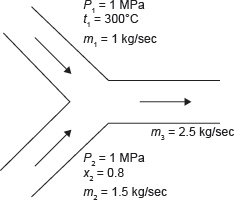
Figure 4.4 Mixing of Two Streams of Steam
Solution:
m2 = m3 – m1 = 2.5 – 1 = 1.5 k/s.
From steady flow energy equation
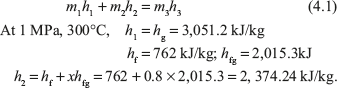
Putting the values of h1 and h2 in Eq. (4.1)
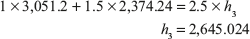
Now enthalpy at 1MPa saturated steam = 2,774.1 kJ/kg = hg
hg > h3
Hence, steam is wet steam
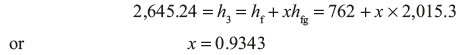
Saturation temperature at 1 MPa = 179.91°C
Example 4.5: At 1.2 MPa, 250°C steam enters into a turbine and expands to 30°C. Determine the work output of turbine for 10 kg/s flow rate steam.
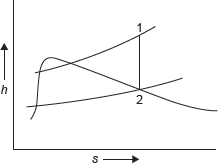
Figure 4.5 h–s Diagram
Solution:
h–s diagram for steam expansion is shown in Figure 4.5.
From steam table, at 1.2 MPa and 250°C
h1 = 2,935 kJ/kg, s1 = 6.8294 kJ/kg K
Since expansion is a diabatic, entropy remains constant
s1 = s2 = 6.8294 kJ/kg K
From saturated steam table, at 30°C
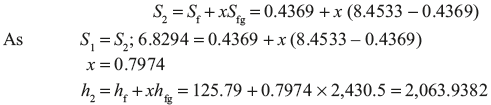
Work output = h1 – h2 = 2,935 – 2,063.93 = 871.06 kJ/kg
For 10kg of steam = 10 × 871.061 = 8,710.61 kJ/kg
Example 4.6: 1.0 kg wet steam of quality 0.7 at 0.3 MPa pressure is heated at constant pressure till the temperature rises to 300°C. Calculate the amount of energy added as heat.
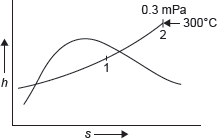
Figure 4.6 h–s Diagram
Solution:
h–s diagram for pressure rise of steam is shown in Figure 4.6.
At point 1 in Figure 4.6
X = 0.7, P1 = 0.3 MPa
From steam table
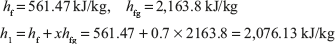
At 0.3 MPa and 300°C, from steam table; h2 = 3,069 kJ/kg
Heat added = h2 – h1 = 3,069.3 – 2,076.13 = 993.17 kJ/kg
Example 4.7: A boiler of volume 10 m3 contains wet steam of quality 0.8 at 0.5 MPa pressure. The inlet and outlet valves of the boiler are closed and the energy addition as heat is stopped. After sometime, the pressure of the steam is found to be 0.2 MPa.
Determine:
- The mass of liquid, mass of vapour in the boiler at the beginning.
- The mass of liquid and mass of vapour in the boiler at the end.
- The energy lost as heat to the surrounding.
From steam table, at 0.5 MPa, saturation temperature, ts = 151.86°C

Solution:
hg = 2,748.7 kJ/kg
Initial internal energy per kg is given by
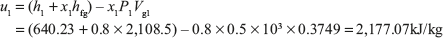
Volume of the boiler is given by V1 = m {x1Vg1 + (1 – x1) Vf1}, where m is mass of steam
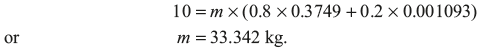
- Thus, mass of steam = 33.42kg × 0.8 = 26.736kg Mass of water = 33.342 × 0.2 = 6.668kgSuppose quality of steam at final state is x2, mx1Vg1 = mx2Vg2Since value of Vf is negligible in the equation x1Vg1 + (1 – x1) Vf1 = x2Vg2 + (1 – x2) Vf2From steam table, at 0.2 MPa,

- Mass of steam = x2 (mw + mg) = x2m = 0.3386 × 33.342 = 11.28 kgMass of water = 33.342 – 11.28 = 22.062
- Final internal energy/kg at 0.2 bar is given by

Heat rejected = Change in internal energy during constant volume process
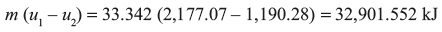
Example 4.8: A pressure cooker contains 1 kg of saturated steam at 6 bar. Find the quantity of heat which must be rejected to reduce the quality of steam to 0.8. Determine the pressure and temperature of steam at the new state.
Solution:

Volume of pressure cooker = 1 kg × Vg1 = 1 × 0.3157 = 0.3157 m3
Volume remains constant, hence, V1 = V2 = 0.3157 m3
Initial internal energy of steam per kg = hg1 – P1Vg1
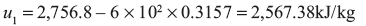
Now suppose quality of the steam at the end is x
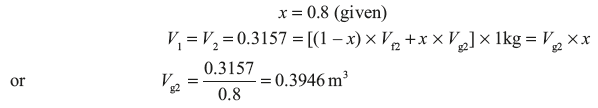
Pressure corresponding to 0.3946 m3/kg = 0.44 MPa (using linear interpolation in steam table value)
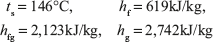
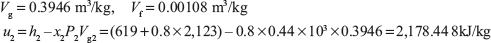
Total heat transfer = 2,178.448 – 2,567.38 = – 1,911kJ
Example 4.9: A sample steam has 5°C as degree of superheat. Before and after throttling, its pressures are 40 and 1 bar, respectively. Calculate the dryness fraction.
Solution:
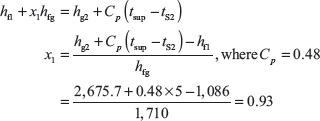


Leave a Reply