Formation Volume Factor

The formation volume factor (B_o), which is also abbreviated FVF, at any pressure may be defined as the volume in barrels that one stock-tank barrel occupies in the formation (reservoir) at reservoir temperature, with the solution gas that can be held in the oil at that pressure. Because both the temperature and the solution gas increase the volume of the stock-tank oil, the factor will always be greater than 1. When all the gas present is in solution in the oil (i.e., at the bubble-point pressure), a further increase in pressure decreases the volume at a rate that depends on the compressibility of the liquid.

It was observed earlier that the solution gas causes a considerable increase in the volume of the crude oil. Figure 2.9 shows the variation in the formation volume factor of the reservoir liquid of the Big Sandy reservoir as a function of pressure at reservoir temperature of 160°F. Because no gas is released from solution when the pressure drops from the initial pressure of 3500 psia to the bubble-point pressure at 2500 psia, the reservoir fluid remains in a single (liquid) state; however, because liquids are slightly compressible, the FVF increases from 1.310 bbl/STB at 3500 psia to 1.333 bbl/STB at 2500 psia. Below 2500 psia, this liquid expansion continues but is masked by a much larger effect: the decrease in the liquid volume due to the release of gas from solution. At 1200 psia, the FVF decreases to 1.210 bbl/STB, and at atmospheric pressure and 160°F, the FVF decreases to 1.040 bbl/STB. The coefficient of temperature expansion for the 30°API stock-tank oil of the Big Sandy reservoir is close to 0.0004 per degrees Fahrenheit; therefore, one stock-tank barrel at 60°F will expand to about 1.04 bbl at 160°F, as calculated from

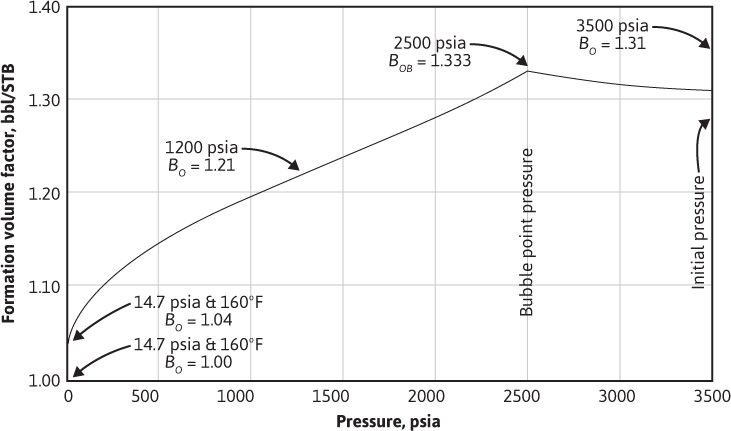
Figure 2.9 Formation volume factor of the Big Sandy Field reservoir oil, by flash liberation at reservoir temperature of 160°F.

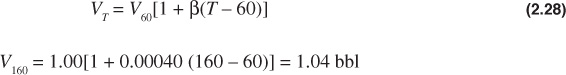
where β is the temperature coefficient of expansion of the oil.

One obvious implication of the formation volume factor is that for every 1.310 bbl of reservoir liquid in the Big Sandy reservoir, only 1.000 bbl, or 76.3%, can reach the stock tank. This figure (76.3% or 0.763) is the reciprocal of the formation volume factor and is called the shrinkage factor. Just as the formation volume factor is multiplied by the stock-tank volume to find the reservoir volume, the shrinkage factor is multiplied by the reservoir volume to find the stock-tank volume. Although both terms are in use, petroleum engineers have almost universally adopted the formation volume factor. As mentioned previously, the formation volume factors depend on the type of gas liberation process—a phenomenon.

In some equations, it is convenient to use the term two-phase formation volume factor (B_t), which is defined as the volume in barrels one stock-tank barrel and its initial complement of dissolved gas occupies at any pressure and reservoir temperature. In other words, it includes the liquid volume, B_o, plus the volume of the difference between the initial solution gas-oil ratio, R_soi, and the solution gas-oil ratio at the specified pressure, R_so. If B_g is the gas volume factor in barrels per standard cubic foot of the solution gas, then the two-phase formation volume factor can be expressed as

Above the bubble point, pressure R_soi = R_so and the single-phase and two-phase factors are equal. Below the bubble point, however, while the single-phase factor decreases as pressure decreases, the two-phase factor increases, owing to the release of gas from solution and the continued expansion of the gas released from solution.

The single-phase and two-phase volume factors for the Big Sandy reservoir fluid may be visualized by referring to Fig. 2.10, which is based on data from Figs. 2.8 and 2.9. Figure 2.10 (A) shows a cylinder fitted with a piston that initially contains 1.310 bbl of the initial reservoir fluid (liquid) at the initial pressure of 3500 psia and 160°F. As the piston is withdrawn, the volume increases and the pressure consequently must decrease. At 2500 psia, which is the bubble-point pressure, the liquid volume has expanded to 1.333 bbl. Below 2500 psia, a gas phase appears and continues to grow as the pressure declines, owing to the release of gas from solution and the expansion of gas already released; conversely, the liquid phase shrinks because of loss of solution gas to 1.210 bbl at 1200 psia. At 1200 psia and 160°F, the liberated gas has a deviation factor of 0.890, and therefore the gas volume factor with reference to standard conditions of 14.7 psia and 60°F is

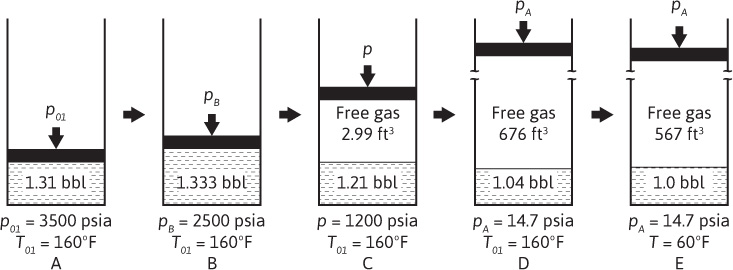
Figure 2.10 Visual conception of the change in single-phase and in two-phase formation volume factors for the Big Sandy reservoir fluid.

Figure 2.8 shows an initial solution gas of 567 SCF/STB and, at 1200 psia, 337 SCF/STB, the difference of 230 SCF being the gas liberated down to 1200 psia. The volume of these 230 SCF is

V_g = 230 × 0.01300 = 2.990 ft³

This free gas volume, 2.990 ft³ or 0.533 bbl, plus the liquid volume, 1.210 bbl, is the total FVF or 1.743 bbl/STB—the two-phase volume factor at 1200 psia. It may also be obtained by Eq. (2.28) as

B_t = 1.210 + 0.002316 (567 – 337)

       = 1.210 + 0.533 = 1.743 bbl/STB

Figure 2.10 (C) shows these separate and total volumes at 1200 psia. At 14.7 psia and 160°F (D), the gas volume has increased to 676 ft³ and the oil volume has decreased to 1.040 bbl. The total liberated gas volume, 676 ft³ at 160°F and 14.7 psia, is converted to standard cubic feet at 60°F and 14.7 psia using the ideal gas law, producing 567 SCF/STB as shown in (E). Correspondingly, 1.040 bbl at 160°F is converted to stock-tank conditions of 60°F as shown in Eq. (2.28) to give 1.000 STB, also shown in (E).

The single-phase formation volume factor for pressures less than the bubble-point pressure may be estimated from the solution gas-oil ratio, oil density, density of the stock-tank oil, and the weighted average specific gravity of the surface gas, using a correlation prepared by McCain, Spivey, and Lenn:¹⁹

where

ρ_o,ST = density of stock-tank oil, lb/ft³

γ_g,S = weighted average specific gravity of the surface gas

ρ_o = oil density

The weighted average specific gravity of the surface gas should be calculated from the specific gravities of the stock-tank and the separator gases from the following equation:

where

γ_g,SP = specific gravity of the separator gas

R_SP = separator gas-oil ratio

γ_g,ST = specific gravity of the stock-tank gas

R_ST = stock-tank gas-oil ratio

For pressures greater than the bubble-point pressure, Eq. (2.32) is used to calculate the formation volume factor:

where

B_ob = oil formation volume factor at the bubble-point pressure

c_o = oil compressibility, psi^–1

Column (2) of Table 2.2 shows the variation in the volume of a reservoir fluid relative to the volume at the bubble point of 2695 psig, as measured in the laboratory. These relative volume factors may be converted to formation volume factors if the formation volume factor at the bubble point is known. For example, if B_ob = 1.391 bbl/STB, then the formation volume factor at 4100 psig is

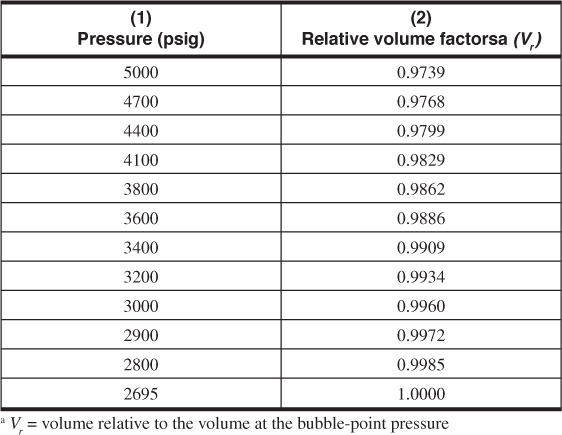
Table 2.2 Relative Volume Data

B_o at 4100 psig = 1.391(0.9829) = 1.367 bbl/STB