The change in volume with pressure for gases under isothermal conditions, which is closely realized in reservoir gas flow, is expressed by the real gas law:
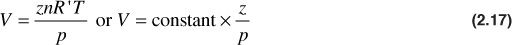
Sometimes it is useful to introduce the concept of gas compressibility. This must not be confused with the gas deviation factor, which is also referred to as the gas compressibility factor. Equation (2.17) may be differentiated with respect to pressure at constant temperature to give
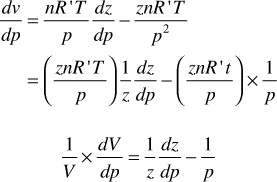
Finally, because
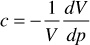

for an ideal gas, z = 1.00 and dz/dp = 0, and the compressibility is simply the reciprocal of the pressure. An ideal gas at 1000 psia, then, has a compressibility of 1/1000 or 1000 × 10–6 psi–1. Example 2.4 shows the calculation of the compressibility of a gas from the gas deviation factor curve of Fig. 2.4 using Eq. (2.18).
Example 2.4 Finding the Compressibility of a Gas from the Gas Deviation Factor Curve
Given
The gas deviation factor curve for a gas at 150°F is shown in Fig. 2.3.
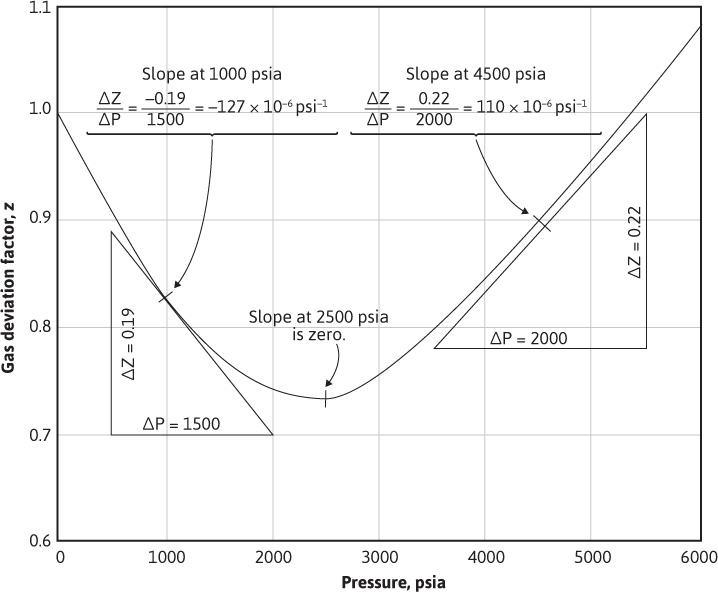
Figure 2.3 Gas compressibility from the gas deviation factor versus pressure plot (see Example 2.4).
Solution
At 1000 psia, the slope dz/dp is shown graphically in Fig. 2.3 as –127 × 10–6. Note that this is a negative slope. Then, because z = 0.83
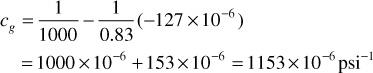
At 2500 psia, the slope dz/dp is zero, so the compressibility is simply
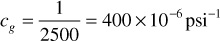
At 4500 psia, the slope dz/dp is positive and, as shown in Fig. 2.3, is equal to 110 × 10–6psi–1. Since z = 0.90 at 4500 psia,
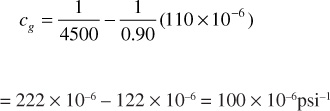
Trube has replaced the pressure in Eq. (2.18) by the product of the pseudocritical and the pseudoreduced pressures, or p = ppc(ppr) and dp = ppcdppr.14 This obtains

Multiplying through by the pseudocritical pressure, the product cg(ppc) is obtained, which Trube defined as the pseudoreduced compressibility (cr):

Mattar, Brar, and Aziz developed an analytical expression for calculating the pseudoreduced compressibility.15 The expression is
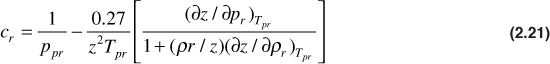
Taking the derivative of Eq. (2.13), the equation of state developed by Dranchuk and Abou-Kassem,10 the following are obtained:
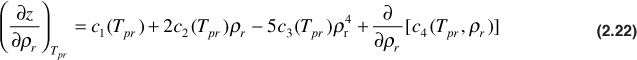
and
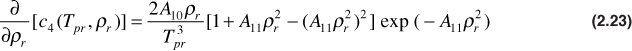
Using Eqs. (2.21) to (2.23) and the definition of the pseudoreduced compressibility, the gas compressibility can be calculated for any gas as long as the gas pressure and temperature are within the ranges specified for the Dranchuk and Abou-Kassem correlation. Using these equations, Blasingame, Johnston, and Poe generated Figs. 2.4 and 2.5.16 In these figures, the product of crTpr is plotted as a function of the pseudoreduced properties, ppr and Tpr. Example 2.5 illustrates how to use these figures. Because they are logarithmic in nature, better accuracy can be obtained by using the equations directly.
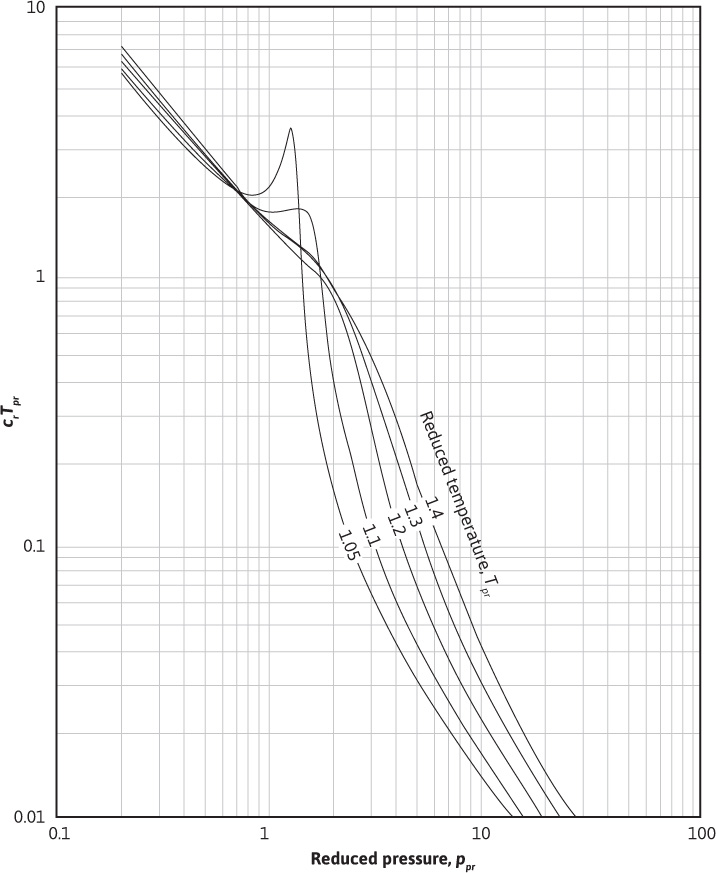
Figure 2.4 Variation in crTpr for natural gases for 1.05 ≤ Tpr ≤ 1.4 (after Blasingame).16
Example 2.5 Finding Compressibility Using the Mattar, Brar, and Aziz Method
Given
Find the compressibility for a 0.90 specific gravity gas condensate when the temperature is 150°F and pressure is 4500 psia.
Solution
From Eq. (2.11) and (2.12), ppc = 636 psia and Tpc = 431°R. Thus,
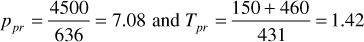
From Fig. 2.5, crTpr = 0.088. Thus,
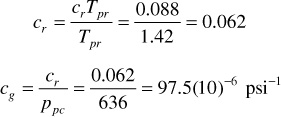
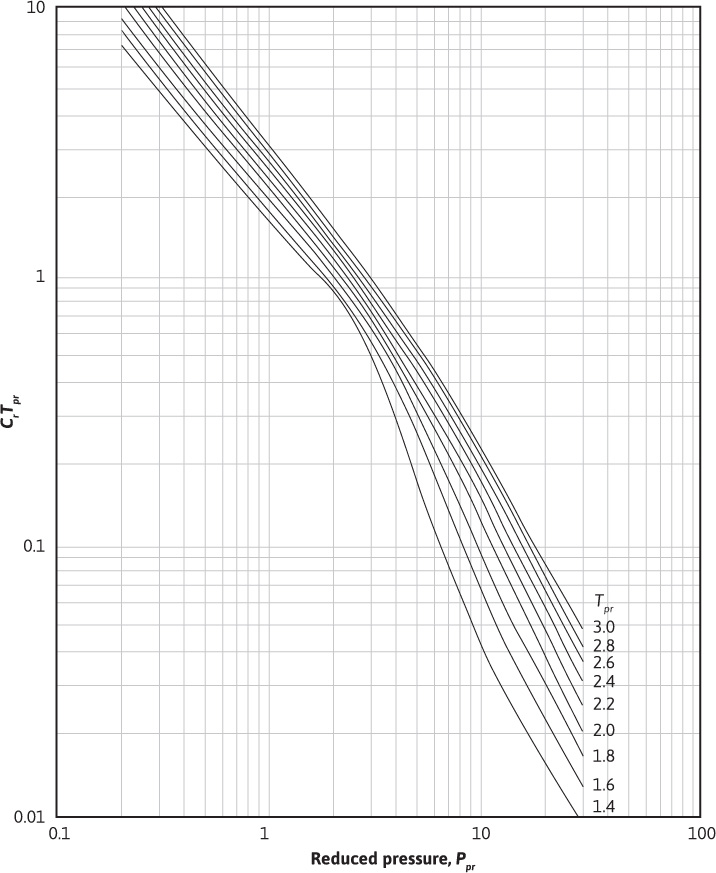
Figure 2.5 Variation in crTpr for natural gases for 1.4 ≤ Tpr ≤ 3.0 (after Blasingame).16
Leave a Reply