In any manufacturing process and operation, variability exists in the process output. In a machining operation, which is one of the most accurate processes, the machined parts may appear to be identical, but close inspection reveals dimensional differences from one part to the next. Manufacturing variations can be divided into two types: random and assignable.
Random variations are caused by many factors: human variability with each operation cycle, variations in raw material, machine vibration, and so on. Individually, these factors may not amount to much, but collectively the errors can be significant enough to cause trouble unless they are within the tolerances for the part. Random variations typically form a normal statistical distribution. The output of the process tends to cluster about the mean value, in terms of the product’s quality characteristic of interest (e.g., length, or diameter, or weight). A large proportion of the population of parts is centered around the mean, with fewer parts away from the mean. When the only variations in the process are of this type, the process is said to be in statistical control. This kind of variability will continue as long as the process is operating normally. It is when the process deviates from this normal operating condition that variations of the second type appear.
Assignable variations indicate an exception from normal operating conditions. Something has occurred in the process that is not accounted for by random variations. Reasons for assignable variations include operator mistakes, defective raw materials, tool failures, machine malfunctions, and so on. Assignable variations in manufacturing usually betray themselves by causing the output to deviate from the normal distribution. The process is no longer in statistical control.
PC relates to the normal variations inherent in the output when the process is in statistical control. By definition, PC equals ±3 standard deviations about the mean output value (a total of six standard deviations):
(8.5)
where PC, process capability; μ, process mean, which is set at the nominal value of the product characteristic; k is the “distance” of control limits from the center line, expressed in standard deviation units. A common choice is k = 3 and σ, standard deviation of the process. Assumptions underlying this definition are (i) the output is normally distributed and (ii) steady‐state operation has been achieved and the process is in statistical control. Under these assumptions, 99.73% of the parts or products produced will have output values that fall with ±3.0 of the mean. This general theory of control charts was first proposed by Dr. Walter A. Shewhart, and control charts developed according to these principles are often called Shewhart control charts.
Statistical Process Control
SPC involves the use of various statistical methods to assess and analyze variations in a process. SPC methods include simply keeping records of the production data, histograms, PC, and control charts. Control charts are the most widely used SPC method, and our discussion in this section will focus on them.
The underlying principle in control charts is that the variations in any process divide into two types (Section 8.4): (i) random variations, which are the variations present if the is in statistical control and (ii) assignable variations, which indicate a departure from statistical control. It is the objective of a control chart to identify when the process has gone out of statistical control, thus signaling that some corrective action should be taken.
A control chart is a graphical technique in which statistics computed from measured values of a certain process characteristic are plotted over time to determine if the process remains in statistical control. The general form of the control chart is illustrated in Figure 8.6. The chart consists of three horizontal lines that remain constant over time: a center, a lower control limit (LCL), and an upper control limit (UCL). The center is usually set at the normal design value. The UCL and LCL are generally set at ±3 standard deviation of the sample means.
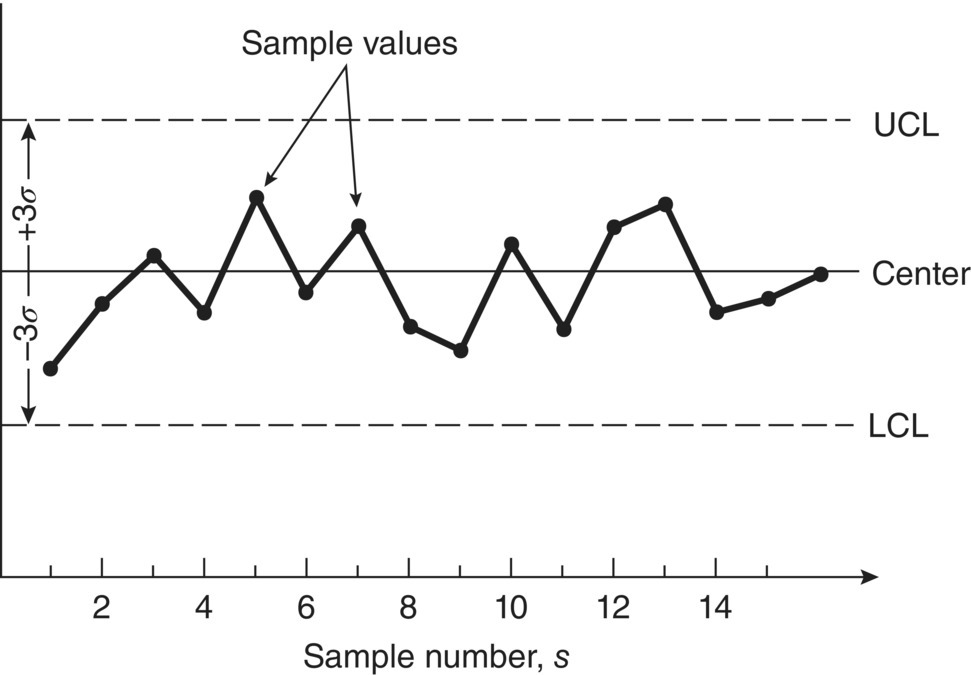
It is highly unlikely that a sample drawn from the process lies outside the UCL or LCL while the process is in statistical control. Thus, if it happens that a sample value does fall outside these limits, it is interpreted to mean that the process is out of control. Therefore, an investigation is undertaken to determine the reason for the out‐of‐control condition, with appropriate corrective action to eliminate the condition. By similar reasoning, if the process is found to be in statistical control and there is no evidence of undesirable trends in the data, then no adjustments should be made, since they would introduce an assignable variation to the process. The philosophy “if it ain’t broken, don’t fix it” is applicable in control charts.
There are two basic types of control charts: (i) control charts for variables and (ii) control charts for attributes. Control charts for variables require a measurement of the quality characteristic of interest. Control charts for attributes simply require a determination of whether a part is defective or how many defects there are in the sample.
Control Charts for Variables
A process that is out of statistical control manifests this condition in the form of significant changes in (i) process mean and/or (ii) process variability. Corresponding to these possibilities, there are two principal types of control charts for variables: (i) 
‐chart and (ii) R‐chart. The 
‐chart (call it “x‐bar chart”) is used to plot the average measured value of a certain quality characteristics for each of a series of samples taken from the production process. It indicates how the process mean changes over time. The R‐chart plots the range of each sample, thus monitoring the variability of the process and indicating whether it changes over time.
A suitable quality characteristic of the process must be selected as the variable to be monitored on the 
and 
charts. In a mechanical process, this might be a shaft diameter or other critical dimension. Measurements of the process itself must be used to construct the two control charts. With the process operating smoothly and absent of assignable variations, a series of samples (e.g. m = 20 or more is generally recommended) of small size (e.g., n = 5 parts per sample) are collected and the characteristics of interest is measured for each part. The following procedure is used to construct the center, LCL, and UCL, for each chart:
- Compute the mean
and range R for each of the m samples. - Compute the grand mean,
, which is the 
values for the m samples; this will be the center for the 
chart. - Compute
, which is the mean of the R values for the m samples; this will be the center for the R chart. - Determine the UCL and LCL for the
and R charts. Values of standard deviation could be estimated from the sample data and used to compute these control limits. However, an easier approach is based on the statistical factors tabulated in Table H.1 that have been derived specifically for these control charts. Values of the factors depends on sample size n. For the 
chart.(8.6)
(8.7)
And for the 
chart,
EXAMPLE 8.7
and 
Charts
Eight samples (m = 8) of size 4 (n = 4) have been collected from a manufacturing process that is in statistical control, and the dimension of interest has been measured for each part. It is desired to determine the values of the center, LCL, and UCL to construct the 
and 
charts. The calculated values of 
and 
for each sample are given below (measured values are in inches), which is step 1 in our procedure.
| s | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
 | 2.008 | 1.998 | 1.993 | 2.002 | 2.001 | 1.995 | 2.004 | 1.999 |
 | 0.027 | 0.011 | 0.017 | 0.009 | 0.014 | 0.020 | 0.024 | 0.018 |
SOLUTION
In step 1, we present constants for the 
and 
in Table 8.1, derived from Table H.1.
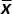
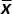and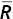 
.In step 2, we compute the grand mean of the sample averages.
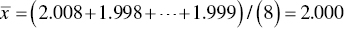
In step 3, the mean value of 
is computed.
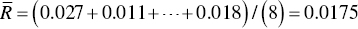
In step 4, the values of LCL and UCL are determined based on factors in Table 8.1. First, using Eqs. (8.6) and (8.7) for the 
chart,
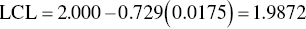
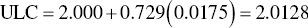
And for the 
chart using Eqs. (8.8) and (8.9)
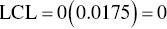
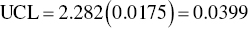
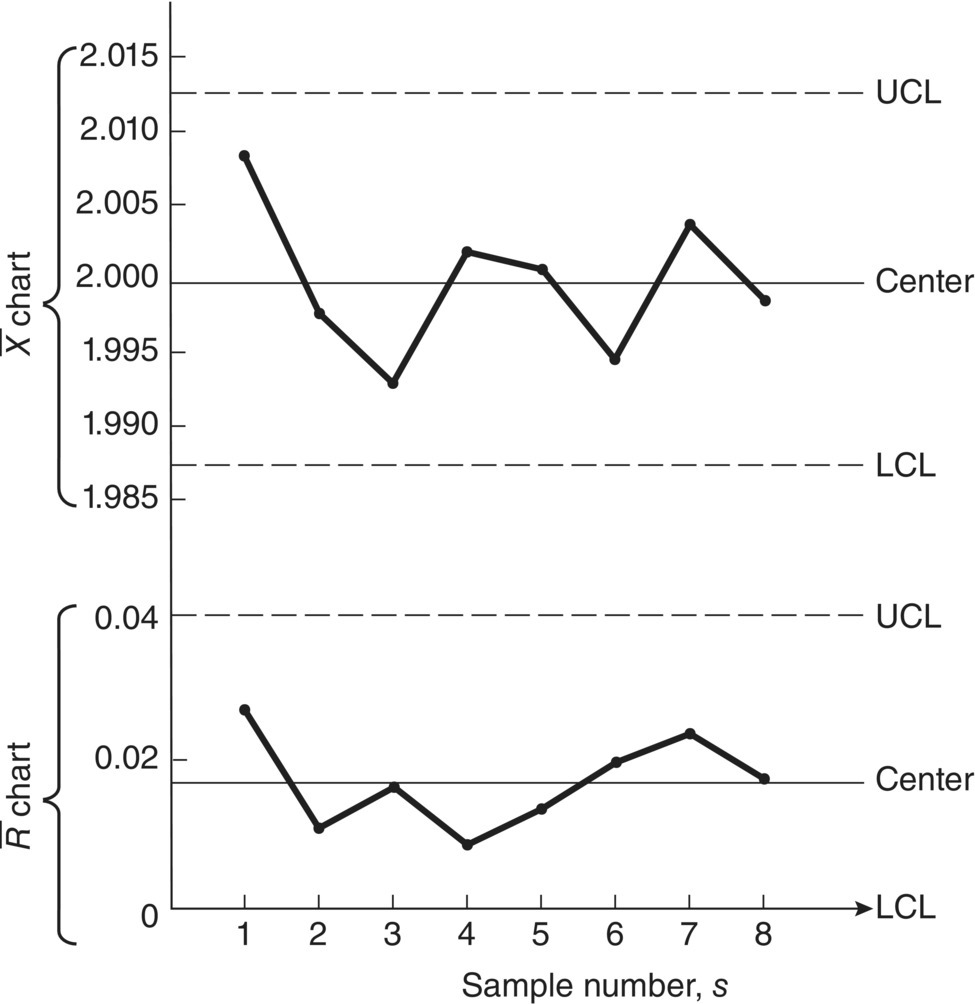
The two control charts are constructed in Figure 8.7 with the sample data plotted in the charts.
If the mean and standard deviation for the process were known, an alternative way to calculate the center, UCL, and LCL for the 
chart would be as follows:
where μ, process mean; σ, standard deviation of the process, and n, sample size. The LCL and UCL values given by Eqs. (8.10) and (8.11) are theoretically the same values as those calculated by Eqs. (8.6)–(8.9). However, when first setting up the 
chart for a process, the mean and standard deviation for the process variable of interest are generally not known. Accordingly, Eqs. (8.6)–(8.9) based on measured 
and 
values can be conveniently used to compute the control chart parameters. With the control limits set at the values defined in Eqs. (8.6)–(8.9) or Eqs. (8.10) and (8.11), 99.73% of the random samples drawn from a process that is in statistical control lie inside the control limits.
Note that the standard deviation of the sample means is related to the population standard deviation by the reciprocal of the square root of n, the number of units in the sample, that is,
(8.12)
where σx, standard deviation of the sample mean and the other terms are as defined above.
PC Analysis
It is usually necessary to obtain some information about analysis of the PC – that is, the performance of the process when it is operating in control. PC is also a mathematical calculation to determine how the manufacturing process (voice of the process) compares with the engineering specifications. The intention is that the engineering specification will match the pressing needs and desires of the customers who use the products and services we produce (voice of the customer). There are several different calculations that have been developed over the years with the most popular ones being the PC ratio (Cp). The Cp can be expressed as an index that is defined as follows:
(8.13)
The numerator of Cp is the width of the specifications. The three‐sigma limits on either side of the process mean are sometimes called natural tolerance limits because these represent limits that an in‐control process should meet with most of the units produced. Consequently, six sigma is often referred to as the width of the process. Cp is the process potential calculation. Cp looks at the engineering specification limits as the numerator and the manufacturing process spread over six standard deviation value. If variable process behavior charts are being used in the manufacturing process, then the range value can be used to estimate the six standard deviations value and the engineering prints will contain the specifications that manufacturing is supposed to work with. The numerical value can never be negative. A value of Cp = 1.0 indicates that the tails of the six standard deviation calculation meet the engineering specification width.
Leave a Reply