Secondary devices are used in conjunction with primary devices to determine the actual flow passing the measuring point. Typically, secondary devices measure the depth of water in the primary device and convert the depth measurement to a corresponding flow, using established mathematical formulas. The output of the secondary device is generally transmitted to a recorder and/or totalizer to provide instantaneous and historical flow data to the operator. Outputs may also be transmitted to sampling systems to facilitate flow proportioning. Secondary devices can be organized into two broad categories:
- A non‐recording type with direct readout (e.g. a staff gauge) or indirect readout from fixed points (e.g. a chain, wire weight, or float)
- A recording type with either digital or graphic recorders (e.g. float in well, float in flow, bubbler, electrical, or acoustic).
Closed Channel Flow
Closed channel flow is normally encountered between treatment units in a WWTP and after lift stations, where liquids and/or sludges are pumped under pressure. It is also encountered in submerged outfalls. Flow in closed channels is usually measured by a metering device inserted into the conduit. Examples of closed channel flow measuring devices are the Venturi meter and the electromagnetic flow meter.
The Venturi meter is one of the most accurate primary devices for measuring flow in closed channels. It is basically a pipe segment consisting of an inlet with a converging section, a throat, and a diverging outlet section, as illustrated in Figure 4.6a. The water velocity is increased in the constricted portion of the inlet section which results in a decrease in static pressure. The pressure difference between the inlet pipe and the throat is proportional to the flow.
Flow in a Venturi meter can be calculated using the equation:
where
- Q = flow (cfs)
- C = discharge coefficient, commonly in the range of 0.90–0.98
- A 2 = cross‐sectional area of throat (ft2)
- g = acceleration of gravity (ft/s2)
- P 1−P 2 = differential pressure (lb/ft2)
- ρ = specific gravity of water (lb/ft3)
EXAMPLE 4.6
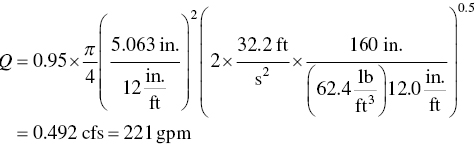
What is the calculated water flow through a Venturi meter with 5.063 in throat diameter when the measured pressure differential is 160 in H2O? Assume C = 0.95 and water temperature of 50 °F.
SOLUTION
Substituting in Eq. (4.7), we obtain
Pitot Tube
Pitot tube or pitot probe (also known as an impact or stagnation tube) is simply a hollow tube that is placed longitudinally in the direction of fluid flow, allowing the flow to enter one end at the fluid’s velocity of approach (Figure 4.6b). It is a pressure measurement instrument used to measure fluid flow velocity and finds uses in both subsonic and supersonic application. Pitot tube is widely used to determine the airspeed of an aircraft, water speed of a boat, and to measure liquid, air, and gas flow velocities at stack and in certain industrial applications. The pitot tube is used to measure the local flow velocity at a given point in the flow stream and not the average flow velocity in the pipe or conduit.
Bernoulli’s equation can be used to predict the static pressure at the stagnation point. Since the velocity of the fluid within the pitot tube is zero, the upstream velocity can be calculated if the static and stagnation pressures are known.
(4.8)
In reality, both friction and heating occur, and the fluid may be compressible. These errors are corrected by a correction factor known as the impact factor, C i, which is applied to the derived velocity. C i is usually very close to 1.00 (e.g. 0.99 or 0.995).
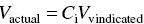
EXAMPLE 4.7
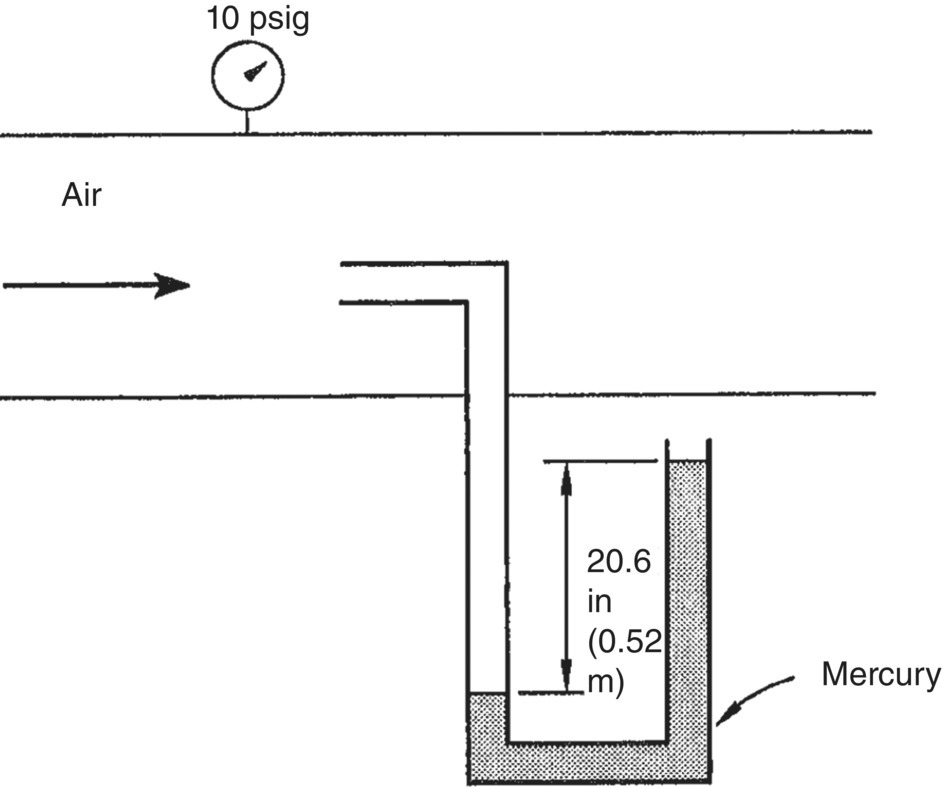
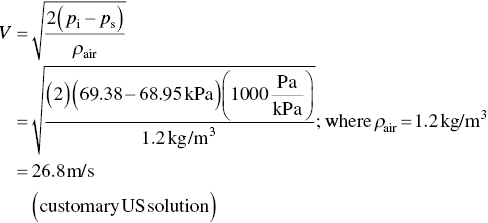
The static pressure of air (0.075 lbm/ft3; 1.2 kg/m3) flowing in a pipe is measured by a precision gauge, shown below, to be 10.00 psig (68.95 kPa). A pitot tube manometer indicates 20.6 in. (0.52 m) of mercury. Losses are insignificant. What is the velocity of the air in the pipe?
SOLUTION IN SI
The density of mercury is 13 600 kg/m3. The impact pressure is
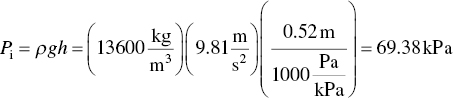
From Eq. (4.9), the velocity is
The pitot tube measures impact (stagnation) pressure. For mercury, pressure in equivalent psi is 0.491 psig/in. Therefore, p i = (20.6 in.)  = 10.11 psig.
= 10.11 psig.
Since impact pressure is the sum of the static and kinetic (velocity) pressure, the kinetic pressure is p v = p i − p s = 10.11 − 10.00 = 0.11 psig, using Eq. (4.10) we get,

Therefore, V = 116.6 ft/s = 117 ft/s (answer).



Leave a Reply