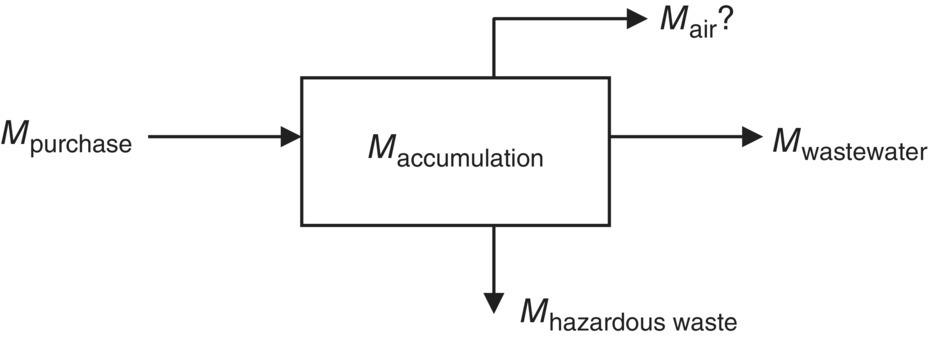
Material balances, also called mass balances and energy balances, are applications of conservation of mass and energy to the analysis of physical systems. Process and equipment selections and sizing require a complete knowledge of all material and energy flow to and from each unit. By accounting for material and/or energy entering and leaving a system, mass and/or flows can be identified which might have been unknown or difficult to measure without this technique. The exact conservation law used in the analysis of the system depends on the context of the problem, but all revolve around mass and energy conservation, i.e. that matter or energy cannot be destroyed or created spontaneously (Haugen et al. 1954; Himmelblau 1998).
The general form quoted for a mass balance is the mass that enters a system must, by conservation of mass, either leave the system or accumulate within the system.
For a steady‐state operation, all operating parameters are time independent, and Eq. (3.21) becomes
(3.22)![]()
Therefore, mass balances are used widely in engineering and environmental analyses. For example, mass balance theory is used to design chemical reactors, to analyze alternative processes to produce chemicals, as well as to model pollution dispersion and other processes of physical systems. In majority of cases, Eq. (3.21) describes material and energy balance around pollution control equipment that is designed for steady‐state operation. Some exceptions to this generalization are encountered in the design of incinerators, direct‐fired dryers, and adsorbers owing to the heat generation and/or pollutant accumulation within the units.
In environmental monitoring, the term budget calculations is used to describe mass balance equations where they are used to evaluate the monitoring data (comparing input and output, etc.) In biology the dynamic energy budget theory for metabolic organization makes explicit use of mass and energy balance.
The following steps are helpful in performing materials and energy balance calculations:
- Draw a sketch of the process
- Identify and label all entering and exiting streams
- Label all pertinent data on the sketch
- Draw a dashed envelope around that portion of the process involved in the balance
- Select a suitable basis for the calculation.
EXAMPLE 3.15 A MASS BALANCE PROBLEM ON HAPS
A manufacturing company has, as part of their first audit, gathered the following data. Estimate the potential annual air emissions in kg of VOCs from the company.
| Purchasing department records | |
| Materials | Purchasing quantity (barrels) |
| Methylene chlorine (CH2Cl2) | 228 |
| Trichloroethylene (C2HCl3) | 505 |
| Wastewater treatment plant influent | ||
| Materials | Average concentration (mg/l) | |
| CH2Cl2 | 4.04 | |
| C2HCl3 | 3.25 | |
| (Average flow into wastewater treatment plant is 0.076 m3/s) | ||
| Hazardous waste manifests | ||
| Materials | Barrels | Concentration |
| CH2Cl2 | 228 | 25 |
| C2HCl3 | 505 | 80 |
| Unused barrel at end of year | ||
| CH2Cl2 | 8 | |
| C2HCl3 | 13 | |
SOLUTION
The mass balance equation would be
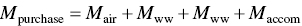
Solving this equation for Mair gives us the estimated VOC emission.
First, we calculate the mass purchased. The eternity of Earth compound is given below.
Mass purchased
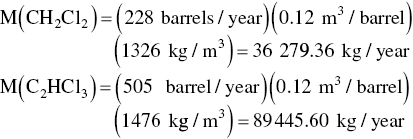
Now we calculate the mass received at the wastewater treatment plant (note that mg/l = g/m3).
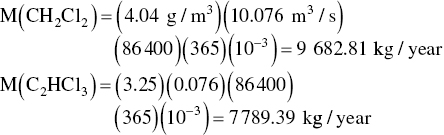
The mass shipped to the hazardous waste disposed facility is calculated next
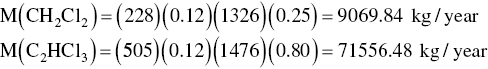
Accumulated
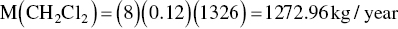
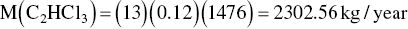
The estimated air emission for each compound is then

EXAMPLE 3.16 HEAT RECOVERY AND SAVE MONEY
Exhaust gas from a chemical process flows at a rate of 8000 acfm from point A at 250 °F and 1 atm pressure. It flows through a circular duct to a fan where the pressure is boosted to 4 inches of water (gage) and then flows to an incinerator. Fuel gas is burned at a rate of 75 lb/h and the temperature of the incinerator exhaust gas is 1200 °F. Assuming both the process exhaust and the incinerator exhaust streams have properties similar to air, calculate the enthalpy that has been added by burning the fuel gas (Btu/h). Assume that you can recover heat from the incinerator exhaust by buying a heat exchanger to cool the gases to 500 °F while recovering useful heat. Assuming that such heat is worth $7.00/million Btu, how much money could you save by recovering that amount of heat ($/day)?
Given:
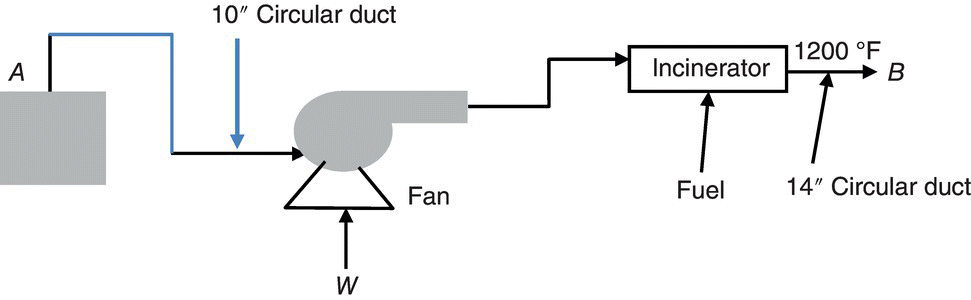
- Q = 8000 cfm
- T1 = (250 + 460)°R = 710 °R
- T2(1200 + 460)°R = 1.66 × 103 °R
- P = 1 atm = 2.12 × 103 psf
- Rc = (0.7302 atm ft3)/(mol. °R)
- Fuel_Feed_Rate = 75 lb/h
SOLUTION
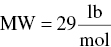
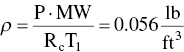
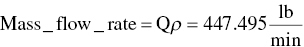
 (From Table C.4)
(From Table C.4)
Calculate mass flow rate from ideal gas law:
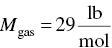
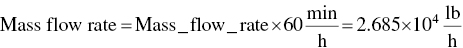
- ∆Hfuel = Mass flow rate × ∆H
Calculate value of recovered heat
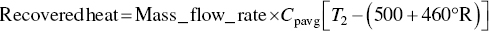
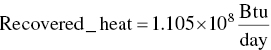
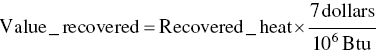
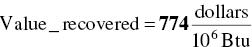
EXAMPLE 3.17 HAZARDOUS WASTE MASS BALANCE FOR MEETING REGULATORY CRITERION
A solvent distilling and recycling, which primarily recycles TCE, is under investigation for the toxic air emissions. As the hazardous waste manager at the site, your goal is to account for the solvents coming in and out into the facility using a waste audit based on a mass balance. The wastes coming into the facility over a one‐year period include the following:
| Invoice number | Volume (l) | TCE concentration (mg/l) |
| 204 | 10 000 000 | 130 |
| 205 | 5 000 000 | 210 |
| 206 | 5 000 000 | 200 |
These aqueous solutions were distilled to concentrate the TCE. The concentrated product was then shipped (over the same one‐year time period) from the facility in tanker trucks as 90% (900 g/l) formulations (the other 10% were various impurities):
| Shipping no. | Volume (l) | TCE concentration (mg/l) |
| 1021 | 2200 | 900 |
| 205 | 1400 | 9000 |
The state regulatory agency allows 200 kg/year TCE emitted into the air from your facility. Using a materials balance, show that the plant is meeting this regulatory criterion.
SOLUTION
- Waste in (over a one‐year period):

- Waste out (over a 1‐year period):

Therefore, volatile losses = 3350 – 3240 = 110 kg (over a one‐year period)
- Answer: Because volatile losses are less than 200 kg/year, the plant is meeting the regulatory criterion.
EXAMPLE 3.18
A 600 MW coal‐fired power plant has an overall thermal efficiency of 38%. It is burning coal that has a heating value of 12 000 Btu/lb, an ash content of 5%, a sulfur content of 3.0%, and a CO2 emission factor of 220 lb/million Btu. Calculate the heat emitted to the environment (Btu/s), the coal feed rate (T/day), the degree (%) of sulfur dioxide control needed to meet an emission standard of 0.15 lbSO2/million Btu of heat input, and the CO2 emission rate (MT/day).
GIVEN:
- Net_power_output = 600 MW
- Thermal_efficiency = 0.38
- Coal_heating_value = 12 000

- Coal_ash_content = 0.05
- Coal_sulfur_content = 0.03
- CO2_emission_factor = 220

SOLUTION
Calculate heat emission (Btu/s)
- Net_power_output = 5.687 × 105

- Heat_out = Power_in_Net_power_output = 9.279 × 105

Calculate coal feed (T/day)
- Coal_feed_rate =
 = 5.388 × 103
= 5.388 × 103
Calculate SO2 removal requirement:
- S + O2 ⇌ SO2





Calculate CO2 emission rate (MT/day)
- CO2_emissions = CO2 emission_factor_coal heating_value_coal_feed_rate
- One metric ton = 1 MT = 1000 kg

Leave a Reply