In some flow process, mass flow rate is not steady but varies with respect to time. In such a case, the difference in energy flow is stored in system as ΔEv.
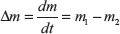
Rate of energy increase = Rate of energy inflow − Rate of energy outflow
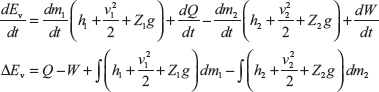
Example 1.14: An air conditioning system, as shown in Figure 1.8, handling 1 kg/s of air at 37°C and consumes a power of 20 kW and rejects heat of 38 kW. The inlet and outlet velocities of air are 50 and 80 m/s, respectively. Find the exit air temperature, assuming adiabatic conditions. Take Cp of air as 1.005 kJ/kg.
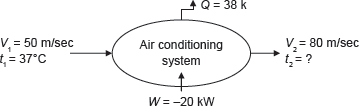
Figure 1.8 Air Conditioning System
Solution:
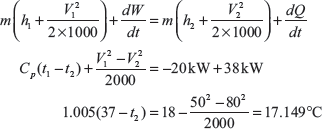
Example 1.15: In a cooling tower of a power plant (Figure 1.9), air enters at a height of 1 m above the ground and leaves at 8 m. The inlet and outlet velocities are 18 and 27 m/s, respectively. Water enters at a height of 10 m and leaves at a height of 0.5 m. The velocity of water at entry and exit are 5 and 1.5 m/s, respectively. Water temperatures are 85 and 42°C at inlet and exit, respectively. Air temperatures are 27 and 70°C at entry and exit, respectively. The cooling tower is fully insulated and a fan of 2.5 kW drives air through the cooler. Find the air per second required for 1 kg/s of water flow. The values of Cp of air and water are 1.005 and 4.18 kJ/kg K, respectively.
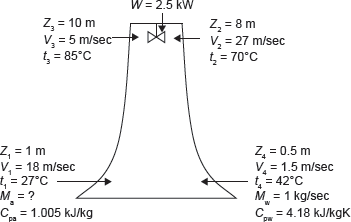
Figure 1.9 Cooling Tower
Solution:
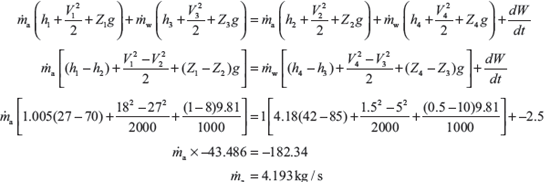
Example 1.16: In a centrifugal air compressor, initial pressure, and specific volume are 1 bar and 1 m3/kg, respectively. The air flow rate is 30 kg/min. Heat liberated to atmosphere from compressor is 100 kW and inlet velocity of air = 10 m/s, outlet velocity of air = 5 m/s. Find
- Compressor work.
- Ratio of inlet and outlet area, if internal energy at outlet is 100 kJ more than that of inlet. Solve the problem using SFEE.
Example 1.17: Air enters in a compressor at the rate of 0.5 kg/s, at 8 m/s with a pressure of 1 bar and a specific volume of 0.85 m3/kg, and leaving at 5 m/s with a pressure of 6 bar and a specific volume of 0.2 m3/kg (Figure 1.10). The internal energy of the air leaving is 80 kJ/kg greater than that of the air entering. Cooling water in a jacket surrounding the cylinder absorbs heat from the air at the rate of 70 W. Calculate the power required to drive the compressor and the inlet, and outlet cross-sectional areas.
Solution:
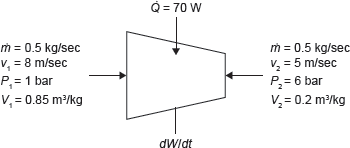
Figure 1.10 Compressor
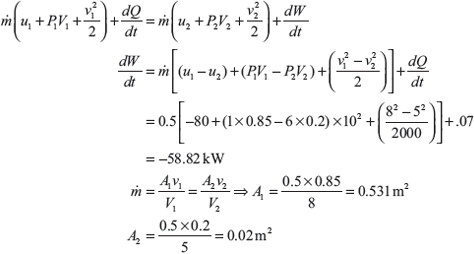

Leave a Reply