In this process, the law is governed by PVn = constant.
Work done during adiabatic process
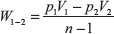
From first law of thermodynamics
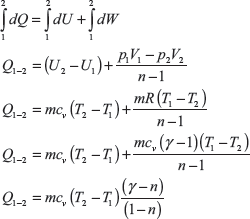
Example 1.2: The initial pressure and temperature of 1 mole of an ideal gas are 1 MPa and 380 K, respectively. It is heated at constant pressure till the temperature is doubled and then is allowed to expand reversibly and adiabatically till the temperature is reduced to 380 K as shown in Figure 1.4, find the heat transferred and work interaction. If it is required to restore the system from final state to original state by a reversible isothermal path, determine the amount of work to be done on system.
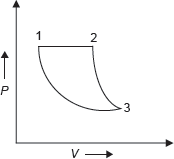
Figure 1.4 P–V Diagram
Solution:
P–V diagram for the process is shown in Figure 1.4.
Let P1 = 1MPa, Tl = 380K, T2 = 2, Tl = 2 × 380 = 760K
Since from 1 to 2 pressure is constant
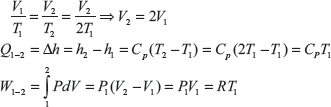
Change in internal energy in the process 2 to 3,
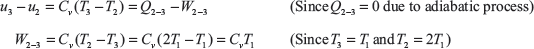
For the process 2 − 3
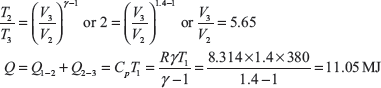
here Q2–3 = 0,
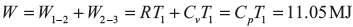
For the reversible isothermal process
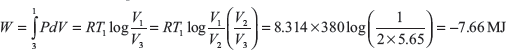
Example 1.3: A system undergoes the cyclic process abcde. The values of Q, W, and Δu for the individual process are as follows:
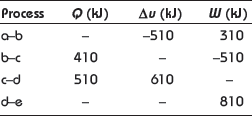
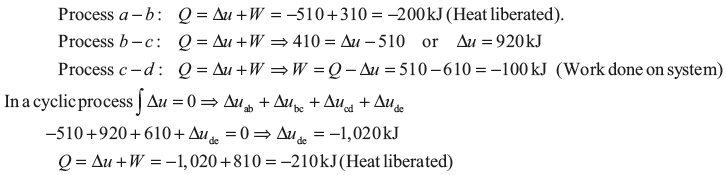
Example 1.4: There is a cylinder-piston system in which pressure is a function of volume as P = x + yV and internal energy is given by u = 36 + 3.16PV, where u is in kJ, P is in kN/m2, V is in m3. If gas changes state from 150 kN/m2 and 0.02 m2 to 350 kN/m2 and 0.04 m2, find the heat and work interaction.
Solution:
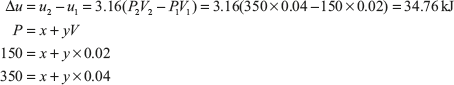
On solving these two equations, we get x = −50 kN/m2 and y = 10,000 kN/m2
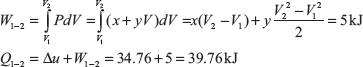
Example 1.5: Calculate the quantities of work if initial pressure and volume are 15 bar and 15 m3 and final volume 25 m3. The process is non-flow reversible as (i) P = constant; (ii) V = constant; (iii) PV = constant; (iv) PVn = constant, where n = 1.3; and (v) PV γ = constant, where γ = 1.4.
Solution:
Example 1.6: A cylinder consists of a frictionless spring loaded piston as shown in Figure 1.5; the pressure of gas at an instant is 5 bar. The spring force exerted on the piston is proportional to the volume of gas. Also, additional atmospheric pressure of 1 bar acts on spring side of piston as shown in Figure 1.5. Calculate the work done by gas in expansion from 0.2 to 0.8 m3.
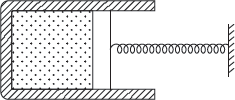
Figure 1.5 Cylinder Piston Arrangement
Solution:
The pressure exerted on spring by the piston,

Example 1.7: A cylinder fitted with a piston has an initial volume of 0.1 m3 and contains nitrogen at 150 kPa, 25°C. The piston is moved compressing the nitrogen until the pressure becomes 1 MPa and temperature becomes 150°C. During the compression process heat is transferred from nitrogen and work done on nitrogen is 20 kJ. Determine the amount of this heat transfer. Assume R = 2,968 J/kg K and Cv = 743 J/kg.
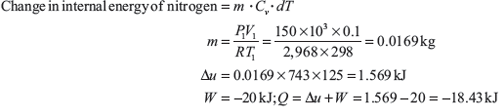
Example 1.8: Figure 1.6 shows two reversible process a − b − c − a and a − d − c − a. Change in internal energy from c to a is 50 kJ and work done by the system during the process a − d is 30 kJ. Find
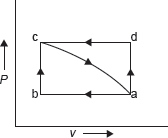
Figure 1.6 P–V Diagram
- Heat interaction during the process a − b − c.
- Heat interaction during the process a − d − c if work done during d − c is 10 kJ.
- Heat interaction during the process c − a if work done on the system during the process c − a is 20 kJ.
Solution:
Example 1.9: A hydraulic brake is used to test an engine at speed of 1,200 rpm. The measured torque of the engine is 15,000 N m and the water flow rate is 0.8 m3/s, its inlet temperature is 15°C. Calculate the water temperature at exit, assuming that the whole of the engine power is ultimately transformed into heat which is absorbed by the water flow.
Solution:
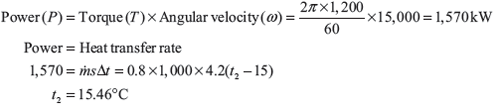
Example 1.10: In a cyclic process, amount of heat transfers are given as 15J, −27, −4 and 32 kJ. Calculate the net work done in the cyclic process.
Solution:
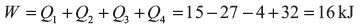
Example 1.11: In a cyclic process, an engine engages in two work interactions: 18 kJ to the fluid and 48 kJ from the fluid, and two heat interactions out of three are given as: 80 kJ to the fluid and 44 kJ from the fluid. Find the magnitude and direction of the third heat transfer.
Solution:
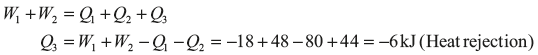
Example 1.12: During a certain period of analysis, a refrigerator consuming the energy at the rate of 1.5 kJ/h loses internal energy of its system by 4,500 kJ. Calculate the heat transfer for the system for that period.
Solution:
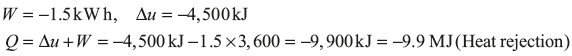
Example 1.13: Two kilograms of water having a constant specific heat 4.18 kJ/kg K is stirred in a well-insulated jar results in rise of temperature by 18°C. Find the Δu and W of the process.
Solution:
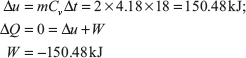








Leave a Reply