BRAESS’ PARADOX FOR TRAFFIC NETWORKS

The result of the collective interaction of noncooperative players may be occasionally quite surprising. We illustrate here a little example of the Braess’ paradox for traffic networks.¹⁸ Imagine a traffic network consisting of links such as road segments, bridges, and whatnot. Most of us had some pretty bad experiences with traffic jams. Intuition would suggest that adding a link to the network should improve the situation or, to the very least, should not make things worse.

Consider the network in Fig. 14.4.¹⁹ In Fig. 14.4(a) we have a four-node directed network, where the following costs are associated with each arc:

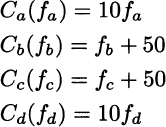
The meaning of these costs should be clarified: They are the traveling costs for an individual driving along each arc, where the flows f_a, f_b, f_c and f_d are the total number of drivers using the corresponding arc. Keep in mind that in game theory the payoff to each player depends on the decisions of the other players as well, and players do not cooperate. In fact, the paradox applies to a problem where drivers have to choose a path independently of each other, but they interact through the level of congestion. This is not a classical network flow problem, where a centralized planner optimizes the overall flow minimizing total cost. Each driver selects a route in a noncooperative way, and we should look for an equilibrium. Traffic equilibrium is beyond the scope but we may take advantage of the symmetry of the example above. Imagine that the total travel demand is 6, i.e., there are six drivers that must go from node 1 to node 4. There are two possible paths, i.e., sequences of arcs: P₁ = (a, c) and P₂ = (b, d). Let us denote by  and  the traffic flows along each path at equilibrium. The cost for path P₁ is

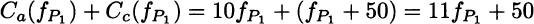
But this happens to be the same as the cost for path P₂:

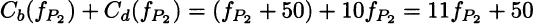
Since the problem is symmetric, intuition suggests that, at equilibrium, the total travel demand is split in two: . Then, the cost of each path for each driver is

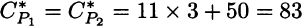
No single driver has an incentive to deviate, because if a driver switches to the other path, her cost would rise to 11 × 4 + 50 = 94. Hence, this is a Nash equilibrium.

Now consider the network 14.4(b), where arc e has been added, whose cost is

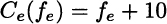
Now, we have an additional path P₃ = (a, e, d). Having opened a new route, some drivers have an incentive to deviate. For instance, if a driver moves from path P₁ to path P₃, her cost would be

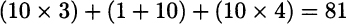
What new equilibrium will emerge? Let us try a symmetric solution again: . At this level of flow, the costs of the three paths are

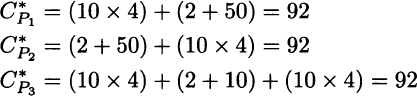
We observe that the three costs are the same, and no one has an incentive to deviate. However, with this equilibrium, every driver is worse off!

The peculiarity of the example above might suggest that this kind of problem is too pathological to actually arise. However, real-life cases have been reported in the literature, where closing a link in a network has improved the situation or adding a new one has created a congestion.²⁰ The crux of the problem, once again, is the collective behavior of several noncooperative decision makers. In business management, this is a common occurrence that should not be dismissed.