Equilibrium in dominant strategies

Sometimes, it is fairly easy to argue which outcome is to be expected. If we consider the strategies for firm A in Table 14.1, we see that:

• If firm B plays high, firm A is better off by playing low, since the payoff 3 is larger than 2.
• If firm B plays low, firm A is better off by playing low, since the payoff 1 is larger than 0.

So, whatever firm B plays, firm A is better off by playing low. The symmetry of the game implies that the same consideration applies to firm B, which will also play low. If there is a single strategy that is preferred by a player, whatever the other players do, it is fairly easy to predict her move. A formalization of this observation leads to the concept of dominant strategy.¹³

DEFINITION 14.1 (Strictly dominant strategy) A strategy  strictly dominates strategy  for player i if

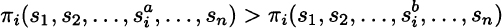
for any possible combination of strategies selected by the other players. There is a strictly dominant strategy  for player i if it strictly dominates all of the alternatives:

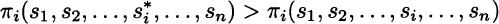
for all alternative strategies  of player i and for all possible strategies S_j of players j ≠ i.

In the above definition we only consider strict domination, which involves strict inequalities. For the sake of brevity, in the following we will often just speak of dominant or dominated strategies, leaving the “strict” qualifier aside; actually, some results in game theory do require strict dominance, but we will not be too precise. Clearly, dominant strategies need not exist, but if one exist for a player, it is an easy matter to predict her behavior. It is also important to notice that, in such a case, the prediction assumes only player’s rationality, and there is no overly stringent requirement concerning what she knows or assumes to know about the other players. Furthermore, if there is a dominant strategy for each player, it is also easy to predict the overall outcome of the game.

DEFINITION 14.2 (Equilibrium in dominant strategies) An outcome  is an equilibrium in dominant strategies if  is a dominant strategy for each player i, i = 1, …, n.

If an outcome is an equilibrium in dominant strategies, given that no rational player will play a dominated strategy, it is sensible to predict that this outcome will be the result of the game. In the prisoner’s dilemma, the strategy low is dominant for both players, and we may argue that the outcome will indeed be (low, low). An important observation is that the resulting payoff for the firms is (1, 1); if the two firms selected (high, high), the payoff would be (2, 2), which is higher for both players. Using the terminology of multiobjective optimization,¹⁴ the second outcome would be preferred by both players and is Pareto-dominant. However, the lack of coordination between players results in a lower payoff to both of them. The problem with the outcome (low, low) is that it is an unstable equilibrium. Incidentally, we observe that certain firms are often prone to collude on prices, and this is exactly why anti-trust authorities have been set up all around the globe; hence, one could wonder if the above prediction makes empirical sense. The key issue here is that we are considering only a one-shot game. Collusion may be the outcome of more complicated, as well as more realistic, multistage models that capture strategic interaction between firms.

Table 14.2 Battle of the sexes.

It is reasonable to expect that an equilibrium in dominant strategies may only be found in trivial games. The following is a classical example in which no equilibrium in dominant strategies exists.

Example 14.5 (Battle of the sexes) After a long week of hard work, Romeo and Juliet have to decide how to spend their Saturday afternoon. There are two choices available:

1. Attending a horror movie festival, which we denote as strategy horror and is much preferred by Romeo.
2. Going on a shoe shopping spree, which we denote as strategy shopping and is much preferred by Juliet.

Despite their differences in taste, Romeo and Juliet are pretty romantic lovers, so they would prefer to spend their time together anyway. Their preferences may be represented by the payoffs in Table 14.2. We note that if the two players select different strategies, the payoff is zero to both of them, as they will be alone. If the outcome is (shopping, shopping), the resulting payoff will be 3 to Juliet, who would be very happy, and 1 to Romeo, who at least will spend his time and more with his sweetheart. Payoffs are reversed for outcome (horror, horror). The game is simple enough, and in practice it can be seen as a stylized model of two firms that should agree on a standard to make their respective products compatible; these games are called coordination games. However, it is easy to see that there is no dominant strategy for either player. For instance, Romeo would play horror, if he knew that Juliet is about to play horror; however, if he knew that Juliet is going to play shopping, he would change his mind.

Equilibrium in dominant strategies is based on a very restrictive requirement, but we may try to guess the outcome in a slightly more elaborated way, by assuming that all players are rational and that everything is common knowledge. The idea is iterated elimination of dominated strategies and is best illustrated by an example.

Table 14.3 Predicting an outcome by iterated elimination of dominated strategies.

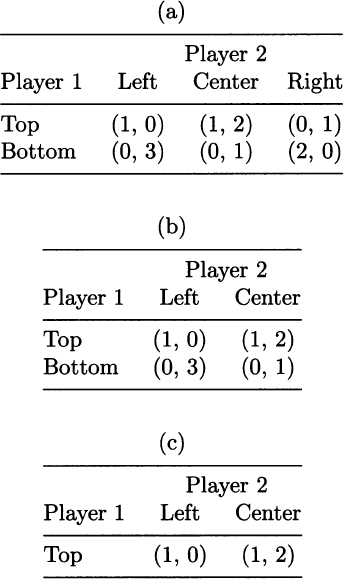
Example 14.6 Consider the game in Table 14.3. Table 14.3(a) describes the game in normal form; note that the row player 1 has two possible strategies, top and bottom, whereas the column player 2 has three available strategies, left, center, and right Let us compare strategies center and right from the viewpoint of player 2. Checking her payoffs, we see that, whatever the choice of player 1, it is better for player 2 to choose center rather than right, as 2 > 1 and 1 > 0; indeed, center dominates right. Eliminating the dominated strategy from further consideration, we obtain Table 14.3(b). By a similar token, from the viewpoint of player 1, we see that strategy bottom is dominated by top, since 1 > 0. Eliminating the dominated strategy, we get Table 14.3(c). Now, we see that the payoff to player 1 is 1 in any case, whereas player 2 will definitely play center, since 2 > 0. Then, we predict the outcome (top, center).

The procedure above sounds quite reasonable. However, a few considerations are in order.

• We should wonder whether the resulting outcome, if any, depends on the sequence that we follow in eliminating dominated strategies. However, it can be shown that strict dominance makes sure that whatever sequence we take, we will find the same result.Table 14.4 Can you trust your opponent’s rationality?
• We may fail to find a prediction, when strict dominance does not apply.
• We have to assume that all players are rational and that everything is common knowledge. This, for instance requires that each of the two players knows that the other one is rational, that she knows that the other one knows that she is rational, and so on. As we pointed out, formalizing the intuitive idea of common knowledge is not quite trivial, but the following example shows that this assumption may be critical.

Example 14.7 Trusting the other player’s rationality can be dangerous indeed. Consider the game in Table 14.4. If player 2 is rational, she should choose the strictly dominant strategy right, because it ensures a payoff 1 > 0, whatever the choice of player 1 is. If we eliminate left, it is easy to see that the outcome should be (bottom, right), since by playing bottom player 1 gets a payoff 2 > 1. However, playing bottom is quite risky for player 1 since, if player 2 makes the wrong choice, his payoff will be –1000.