WHAT IS UNCERTAINTY?

When we flip a fair coin, we are uncertain about the outcome. However, we are pretty sure about the rules of the game: The coin will either land head or tail, and to all practical purposes we assume that the two outcomes are equally likely. However, what about an alien who has never seen a coin and does not take our probabilities for granted? Probably, it would face a more radical form of uncertainty, where the probabilities themselves are uncertain, and not only the outcome of the flip.¹ By a similar token, sometimes we have plenty of reliable and relevant data about a random phenomenon, possibly featuring significant variability, which suggests the application of a frequentist concept of probability. Again, coming up with a good decision in such a setting may be far from trivial, but at least we might feel confident about our representation of uncertainty. Unfortunately, we are not always so lucky. Sometimes, we do not have relevant data, as we are facing a brand-new situation, as is the case when launching a truly innovative product. In other cases, the situation is so risky that we cannot have blind faith in statistical data analysis. How about an event with a very low probability, but potentially catastrophic?

Example 14.1 Suppose that we are interested in investigating the safety of an airport, in terms of its ability to manage the takeoff–landing traffic. Apparently, we should consider the statistics of accidents that may be blamed on the airport. However, hopefully, data on such accidents are so scarce that they are hardly relevant. In such a case, we should also consider the near misses, i.e., events that did not actually result in a disaster, but indicate that something is not working as it should. By the same token, car insurance companies are also interested in the driving habits of a potential customer, and not only in his accident track record.

This example shows that sometimes past statistics are not quite relevant because of lack of data. In other cases, even if we have plenty of data, a structural change in the phenomenon may make them irrelevant. We have pointed out that there are different interpretations of probabilities. Indeed, the cases above illustrate both the classical concept of probability, based on the idea that there are underlying equally likely outcomes, and the frequentist concept. However, probability may also be a measure of belief in a scientific theory, possibly including subjective elements. Some have even questioned the use of probability as a model of uncertainty. Alternative frameworks have been proposed, like fuzzy sets. We will stick to a probabilistic framework, but it is important to understand a few basic issues, with reference to Fig. 14.1. There, we use a familiar scenario tree (or fan) to represent uncertainty. We have to make a decision here and now, but its ultimate consequence depends on which future scenario will occur. According to a simple probabilistic view, each scenario S_i is associated with a well-known probability π_i, i = 1, 2, 3. Unfortunately, things are not always that easy.

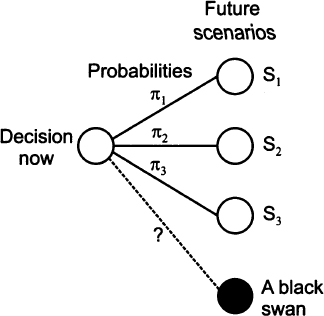
Fig. 14.1 Schematic illustration of different kinds of uncertainty.