The idea that most decision makers are risk-averse is intuitively clear, but what does risk aversion really mean? A theoretical answer, commonly put forward in economic theory, can be found by assuming that decision makers order uncertain outcomes by a utility function rather than by straightforward expected monetary values. To introduce the concept, let us consider simple lotteries. A lottery is represented by a random variable X that assumes values xi with probabilities pi; the decision maker should select among alternative lotteries and may also combine them, forming new random variables. For instance, consider an agent who has to choose between the following two lotteries:
- Lottery a1, which is actually deterministic and has a sure payoff μ.
- Lottery a2, which has two equally likely payoffs μ + δ and μ − δ.
The two lotteries are clearly equivalent in terms of expected payoff, but a risk-averse agent will arguably select lottery a1. More generally, if we have a random variable X and we add a mean-preserving spread, i.e., a random variable 
with 
, this addition is not welcome by a risk-averse decision maker.
Given a set of lotteries, the agent should be able to pick the preferred one; more precisely, given any pair of lotteries, the agent should be able to tell which one she prefers or decide that she is indifferent to a choice between them. If so, we have a preference relationship among lotteries. Since preference relationships are a bit cumbersome and are not easy to deal with, we could map each lottery to a number, measuring the attractiveness of that lottery to the agent, and use the standard ordering of numbers to rank lotteries. For arbitrary preference relationships, a function representing them may not exist but, under a set of more or less reasonable assumptions,4 such a mapping does exist and can be represented by a utility function. A particularly simple form of utility function, which looks reasonable but is justified by specific hypotheses on the preference relationship that it models, is the Von Neumann-Morgenstern utility, defined as
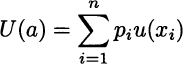
The definition involves a function u(·), and a is a lottery with n outcomes xi and probabilities pi. The function u(·) is the utility of a certain payoff, and U(·) is the expected utility. If u(x) ≡ x, then the utility function boils down to the expected value of the payoff. Alternative choices of the utility function u model different attitudes toward risk. For business problems, it is reasonable to assume that utility u(·) is an increasing function, since we prefer more wealth to less.
In the case of the two lotteries above, preference for a1 is expressed by
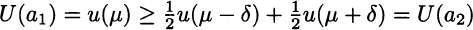
Since the inequality is not strict, we should say that lottery a1 is at least as preferred as a2, and the decision maker could be indifferent between the two. More generally, if we have two possible outcomes, x1 and x2, with probabilities P1 = p and p2 = 1 − p, respectively, a risk-averse decision maker would prefer not taking chances:
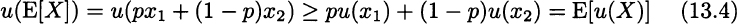
This condition basically states that the function u(·) is concave. Figure 13.6 illustrates the role of concavity. In Theorem 6.8 we have introduced Jensen’s inequality for convex functions. Indeed, Eq. (13.4) is just a specific case of Jensen’s inequality for concave functions of a random variable X:
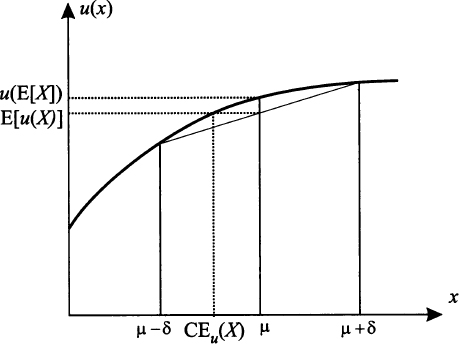
Fig. 13.6 How concave utility functions imply risk aversion; the certainty equivalent is also shown.
It is fundamental to observe that the specific numerical value that the utility function assigns to a lottery is irrelevant per se; only the relative ordering of alternatives is essential. In fact, we speak of ordinal rather than cardinal utility. Given the linearity of expectation, we also see that an affine transformation of the utility function u(·) has no effect, provided it is increasing: If we use au(x) + b instead of u(x), where a > 0, the relative ranking of alternatives is preserved.
How can we say something about the properties of a specific utility function? In particular, we would like to come up with some way to measure risk aversion. We have said that a risk-averse decision maker would prefer a certain payoff rather than an uncertain one, when the expected values are the same. She would take the gamble only if the expected value of the risky lottery were suitably larger than the certain payoff. In other words, she requires a risk premium. The risk premium depends partly on the risk attitude of the decision maker, and partly on the uncertainty of the gamble itself. We will denote the risk premium by ρu(X); note that this is a number that a decision maker with utility u(·) associates with a random variable X. The risk premium is defined by the condition
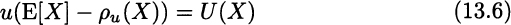
The risk premium implicitly defines a certainty equivalent, i.e., a sure and guaranteed payoff CEu(X) such that the agent would be indifferent between this certain amount and the uncertain lottery:
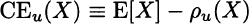
Note that the certainty equivalent is smaller than the expected value, and the difference is larger when the risk premium is larger. These concepts may be better grasped by looking again at Fig. 13.6.
A difficulty with the risk premium concept is that it mixes the intrinsic risk of a lottery with the risk attitude of the decision maker. We might wish to separate the two sides of the coin. Consider a lottery 
, where x is a given number, and 
is a random variable with 
and 
. Assume that the random variable is a “small” perturbation, in the sense that any possible realization is a relatively small number.5 Hence, we may approximate both sides of Eq. (13.6) by Taylor’s expansions. Consider, for instance, the expression 
. Since only numbers are involved here, we may write
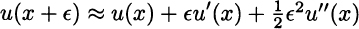
Using this approximation for the random variable , under the assumption that its realization are small enough, and taking expected values, we may approximate the right-hand side of (13.6) as follows:
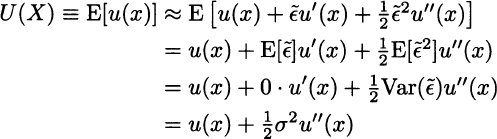
In the second-to-last (penultimate) line we have used 
. We may also approximate the left-hand side of (13.6), which involves only numbers, by a first-order expansion around E[X] = x:
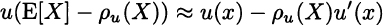
Equating the two approximations and rearranging yields
Since we assume the utility function to be concave and increasing, the right-hand side of Eq. (13.7) is positive.6 We observe that the risk premium is factored as the product of one term depending on the subjective agent’s risk aversion and another one depending on the objective uncertainty of the lottery. This justifies the following definition of the coefficient of absolute risk aversion:
We have said that, given the linearity of the expectation operator, transforming the utility function u(x) by an increasing affine transformation is inconsequential. Indeed, the definition of the risk aversion coefficient is consistent with this observation, as it is easy to see that the coefficients for u(x) and au(x) + b are the same. Note that the coefficient 
does not depend on uncertainty, but it does depend on the expected value of the lottery. From an investor’s perspective, this implies that risk aversion depends on the current level of wealth. The more concave the utility function, the larger the risk aversion.
By a similar token, we may define the coefficient of relative risk aversion. This is motivated by considering a multiplicative, rather than additive, shock on an expected value 
. Using a similar reasoning, we get
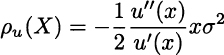
which suggests the definition
Example 13.7 (A few standard utility functions) A typical utility function is logarithmic utility:7
Clearly this makes sense only for positive values of wealth. It is easy to check that, for the logarithmic utility, we have
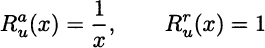
Hence, logarithmic utility has decreasing absolute risk aversion, but constant relative risk aversion. We say that logarithmic utility belongs to the families of decreasing absolute risk aversion (DARA) and constant relative risk aversion (CRRA) utility functions. We may also consider the exponential utility function
for α > 0. Note that this is an increasing function, and it is easy to interpret the parameter α:
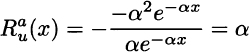
Hence, we see that the exponential utility is constant absolute risk aversion (CARA). It is important to remark that some utility functions have been used because they are easy to manipulate, but this does not imply that they always model realistic investors’ behavior.8
Another common utility function is the quadratic utility:
Note that this function is not monotonically increasing and makes sense only for x ∈ [0, 1/λ]. Another odd property of quadratic utility is that it is increasing absolute risk aversion (IARA):
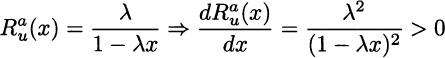
This implies, for instance, that an investor becomes more risk averse if her wealth increases, which is usually considered at odds with standard investors’ behavior. Nevertheless, we may also see that quadratic utility emphasizes the role of variance, since for this utility
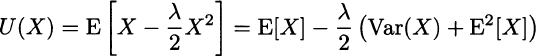
A decision maker with quadratic utility is basically concerned only with the expected value and the variance of an uncertain outcome.
Specifying a utility function may be a difficult task, since assessing the tradeoff between expected payoff and risk is far from trivial. This may be of no concern in economics, if the aim is to build a model explaining some observed behavior and qualitative insights that are of interest; however, in business decision making, it is an issue. In the following sections, we consider more operational approaches.
Leave a Reply