In this section and the next one, we consider the solution of a mathematical programming problem. We will do so essentially for linear programs, continuous and mixed-integer ones, but it is also important to get a feeling for more general, theoretical concepts in nonlinear programming. We will not cover nonlinear programming methods, but we will stress the economic interpretation of some fundamental concepts.
The constrained optimization problem
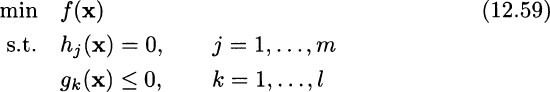
is a nonlinear programming problem if even one function among f, hj, or gk is nonlinear. A stationarity condition for the objective function does not help in finding an optimizer; to see why, a look at the following counterexample suffices:
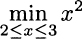
The function is stationary at the origin, but this point is outside the feasible region. The obvious optimizer x* = 2 is not a stationarity point, and it is the lower bound on x that determines the optimal solution. However, assuming that all of the involved functions are well-behaved enough, in terms of differentiability, we can try to generalize stationarity concepts to find candidate optimal points.
Leave a Reply