The standard error of regression

Equations (10.16) and (10.18) help us in assessing the uncertainty about the estimate of unknown regression parameters. A missing piece in this puzzle, however, is the standard deviation  of the random errors, which are not directly observable. The only viable approach we have is to rely on the residuals  as a proxy for the errors . The intuition is that, if we trust the estimated model,  is the expected value of Y_i and, in order to assess the variability of the errors, it is reasonable to consider the variability of the observations with respect to their expected value. Another way to get the picture is by noting that the assumptions behind the statistical model imply that ; however, we cannot just take the usual sample variance of the observed Y_i, since the expected value of Y_i is not a constant, but it depends on the value of x_i. The following result, which holds under our assumptions, helps us in estimating the standard deviation of errors.

THEOREM 10.2 If errors are i.i.d. and normally distributed with standard deviations , then the ratio of SSR (sum of squared residuals) and  is a chi-square random variable with n − 2 degrees of freedom:

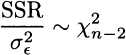
Given what we know about the chi-square distribution,¹² we immediately conclude that an unbiased estimator of the standard deviation of errors is given by the standard error of regression (SER), defined as follows:

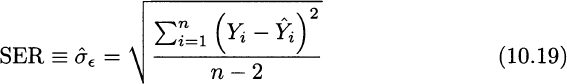
Example 10.6 Let us find the SER for the data in Fig. 10.1. We recall that, in that case, the regressed model was

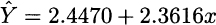
Plugging values of the regressors and computing the residuals yields the results listed in Table 10.2. Then we obtain

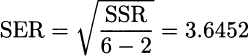
Table 10.2 Residuals for the data of Fig. 10.1.

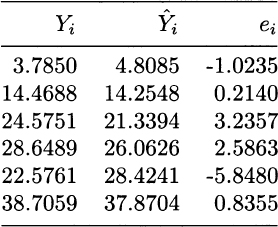
We urge the reader to check that, for the data in Fig. 10.2, we get SER = 15.8114. This much larger SER shows that, even though the regressed models are the same, the underlying errors are quite different.

The definition of SER in Eq. (10.19) is essentially a sample standard deviation, with a couple of twists:

1. Deviations are not taken against a constant value, but with respect to a sort of moving target depending on the regressors x_i.
2. Unlike the usual sample standard deviation, we divide by n − 2 rather than n − 1. The cookbook recipe way of remembering this is that we lose 2 degrees of freedom because deviations depend on two estimated parameters, rather than just the usual sample mean . Also note that if we had just n = 2 observations, we could say nothing about errors, because the observed points would exactly fit one line, and there would be no deviation between Y_i and .