We have already sketched an application of this method in Example 9.34. To state the approach in more generality, let us introduce the sample moment of order k:

The sample moment is the sample counterpart of moment mk = E[Xk]. Let us assume that we need an estimate of k parameters θ1, θ2,…, θk. The method of moments relies on the solution of the following system of equations:
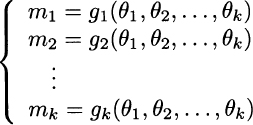
In general, this is a system of nonlinear equations that may be difficult to solve, and we cannot be sure that a unique solution, if any, exists. However, assuming that there is in fact a unique solution, we may just replace moments mk by sample moments Mk, and solve the system to obtain estimators ![]() .
.
Example 9.36 Let X1, X2,…Xn be a random sample from a normal population with parameters (θ1, θ2) ≡ (μ, σ). We know that
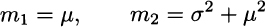
Plugging sample moments and solving the system yields
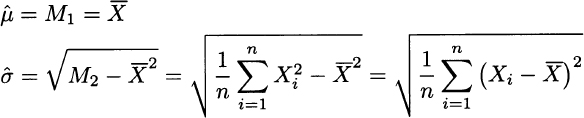
We note that we do not obtain an unbiased estimator of variance.
Leave a Reply