Convergence in probability

The first stochastic convergence concept that we illustrate is not the strongest one, but it can be easier to grasp.

DEFINITION 9.7 (Convergence in probability) A sequence of random variables, X₁, X₂,…, converges in probability to a random variable X if for every 

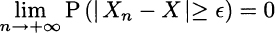
The definition may look intimidating, but it is actually intuitive: X_n tends to X if, for an arbitrarily small , the probability of the event  goes to zero. In other words

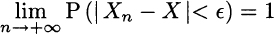
i.e., the difference between the two realizations cannot be larger than a small and arbitrary constant . Convergence in probability is denoted as follows:

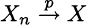
or

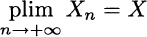
We may also apply the definition to express convergence to a specific number a, rather than a random variable.

Example 9.29 Consider the following sequence of random variables:

We see that, for n going to infinity, X_n may take a larger and larger value n, but its probability is vanishing. Indeed, the probability mass gets concentrated on the value 0 and

Using this concept, we may clearly state (without proof) one form of the law of large numbers.

THEOREM 9.8 (Weak law of large numbers) Let X₁, X₂,… be a sequence of i.i.d. random variables, with E[X_i] = μ and finite variance Var(X_i) = σ² < +∞. Then

As you may imagine, there must be a different, strong form of this law; as we shall see, it uses a stronger form of stochastic convergence. Despite its relative weakness, convergence in probability is relevant in the theory of estimation, in that it allows us to define an important property of an estimator. Consider a sequence of estimators Y_n of an unknown parameter θ; each Y_n is a statistic depending on a sample of size n. We say that this is a consistent estimator if

The weak law of large numbers implies that the sample mean is a consistent estimator of expected value.