STOCHASTIC CONVERGENCE AND THE LAW OF LARGE NUMBERS

In this section we start considering in some more depth the issues involved in inferential statistics. The aim is to bridge the gap between the elementary treatment that is commonly found in business-oriented textbooks, and higher-level books geared toward mathematical statistics. As we said, most readers can safely skip these sections. Others can just have a glimpse of what is required to tackle a deeper study of statistical and econometric models. Furthermore, the usual cookbook treatment is geared towards normal populations, which may result in a distorted and biased perspective. A normal distribution is characterized by two parameters, μ and σ², which have an obvious interpretation as expected value and variance, respectively. As a result, we tend to identify the estimation of parameters with the estimation of expected values or variances. However, this is a limited view. For instance, the beta distribution²³ is characterized by two parameters, α₁ and α₂; if we know those parameters, we may compute whatever moment we want, expected value, variance, skewness, etc. But to estimate these parameters, we cannot just rely on a sample mean. Thus, we need a more general framework to tackle parameter estimation. Indeed, there are a few alternative strategies to obtain estimators. We should understand what makes a good estimator, in order to assess the tradeoffs when alternatives are available. Finally, we have derived confidence intervals and hypothesis testing procedures in a somewhat informal and ad hoc manner. Actually, there are general strategies that help to assess desirable properties of them as well.

We deal with the above issues in the rest and a good starting point to motivate our work is a better investigation of the law of large numbers, which we previewed in Section 7.7.4. Intuitively, if we take a large random sample, the sample mean should get closer and closer to the true expected value. Therefore, we should expect a convergence result loosely stated as follows:

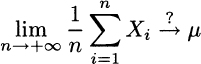
The question mark stresses the fact that this convergence is quite critical: In which sense can we say that a random variable converges to a number? More generally, we could consider convergence of a sequence of random variables X_n to a random variable X. The relevance of a “stochastic convergence” concept to analyze parameter estimation problems for large samples should be obvious. Furthermore, we have illustrated the central limit theorem in Section 7.7.3. There, we loosely stated that a certain random variable “converges” to a normal distribution; we should make this statement more precise. As it turns out, there is not a single and all-encompassing concept of stochastic convergence, which may be defined in a few different ways; they may be more or less useful, depending on the application; furthermore, some convergence concepts may be weaker, but easier to verify.