Estimating skewness and kurtosis

We have defined skewness and kurtosis as:¹⁷

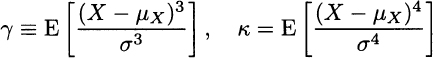
These definitions are related to higher-order moments of random variables. Just like expected value and variance, these are probabilistic definitions, and we should wonder if and how these measures should be estimated on the basis of sampled data. The “if” should not be a surprise. If we know that the sampled population is normal, there is no point in estimating skewness and kurtosis, since we know that γ = 0 and κ = 3 for a normal distribution. By the same token, for other distributions, skewness and kurtosis are related to parameters of the distribution. For instance, a beta distribution is defined in terms of two parameters, α₁ and α₂; any other feature depends on these parameters. Hence, we should really estimate these parameters, rather than the expected value, variance, skewness, or kurtosis. Indeed, we will take this more general view in Section 9.9.

On the contrary, if we do not take a specific distribution for granted, we might be interested in an estimate of skewness and kurtosis. One possible way to estimate these characteristics relies on the definition of higher-order moments.¹⁸ If we denote the central moment of order k by

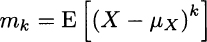
we have

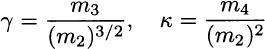
Then, we could consider sample moments of order k

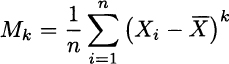
and define sample skewness as follows:

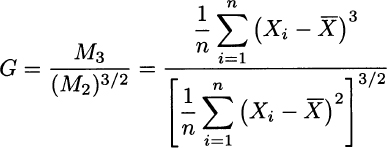
By the same token, we would consider the following definition of sample kurtosis:

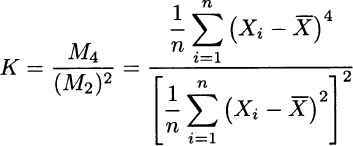
Unfortunately, these are not unbiased estimators of γ and κ. The following corrections are typically used:¹⁹

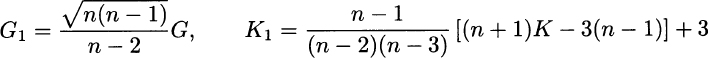
Neither of these adjustments eliminates bias, however; some software packages offer the choice between these two forms of estimator. We stress again that if we assume a given distribution, estimating skewness and kurtosis is a false problem. If we do not take a specific distribution for granted, we might use either form of sample skewness and sample kurtosis to get a feeling for the sensibility of our hypothesis. For instance, if we are checking normality, we should find a sample skewness close to 0 and a sample kurtosis close to 3. If the estimates are quite far from what we expect, we should be inclined to rule out normality; however, even if we find G ≈= 0 and K ≈ 3, this would not be enough to conclude normality. In fact, there are nonparametric tests that can be used to check the plausibility of an assumption about the whole distribution, without referring to specific parameters.