The sample mean is a point estimator for the expected value, in the sense that it results in an estimate that is a single number. Since this estimator it is subject to some variance, it would be nice to have some measure of how much we can trust that single number. In other words, we would like to get an emf interval estimate, which typically comes in the form of a confidence interval. Roughly speaking, a confidence interval is a range in which the true, unknown parameter should lie with some probability. As we shall see, this statement must be taken with due care if we wish a rigorous interpretation, but it is a good declaration of intent. This probability is known as the confidence level, and it should be relatively large, say, 95% or 99%. In this section, we derive a confidence interval for the expected value of a normal distribution or, in more colloquial terms, for the mean of a normal population. Later, we apply the idea to the parameter of a Bernoulli population and to the variance of a normal population.
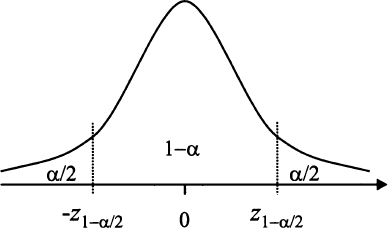
Fig. 9.1 Illustrating the link between quantiles of the standard normal and confidence intervals.
From Section 9.1.1 we know that the statistic
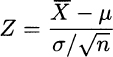
has standard normal distribution, if the sample comes from a normal population with parameters μ and σ2. Note that, if we were so lucky as to get a “perfect” sample, we would have 
and Z = 0. In real life, the sample mean 
will be smaller or larger than the true expected value μ, and Z will be negative or positive, accordingly. Figure 9.1 illustrates the question, in terms of the PDF of a standard normal and its quantiles. There, z1−α/2 is the quantile with probability level 1 − α/2, i.e., a number such that P(Z ≤ z1−α/2 = 1 − α/2. Correspondingly, α/2 is the area of the right tail, to the right of quantile z1−α/2. Given the symmetry of the normal distribution, we observe that P(Z ≤ −z1−α/2) = α/2; i.e., we also have a left tail with probability (area) α/2. Then, by construction, the probability that the Z statistic falls between those two quantiles is as follows:
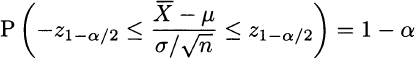
This is just the area under the PDF, between the quantiles. If you prefer, it is the total area, which amounts to 1, minus the areas associated with the left and right tails, each one amounting to α/2. Now, let us rearrange the first inequality:
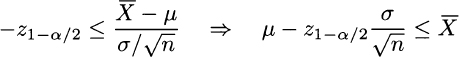
Doing the same with the second inequality and putting both of them together, we conclude that
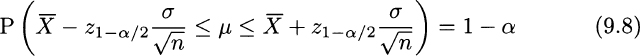
We should note carefully that μ is an unknown number that is bracketed by two random variables with probability 1 − α. Then, we conclude that the interval
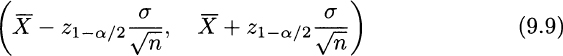
is a confidence interval for the expected value μ of a normal distribution, with confidence level 1 − α. Formula (9.9) is very easy to apply, but there is a little fly in the ointment: It assumes that the standard deviation σ is known. Arguably, if the expected value is unknown, it seems quite unreasonable that standard deviation is known. In fact, however weird it may sound, there are situations in which this happens.
Example 9.7 Imagine that we are measuring a physical quantity with an instrument affected by some measurement uncertainty. Then, what we read from the instrument is a random variable X; if there is no measurement bias, E[X] = μ, where μ is the true value of the quantity we are measuring. We may regard the measurement as 
, where 
is some noise corrupting what we read on the instrument. Unbiasedness amounts to stating 
. If the instrument has been well calibrated using appropriate procedures, we may have a pretty good idea of the standard deviation of each observation, which is actually the standard deviation 
of noise. Hence, we (almost) know the standard deviation of random variable X, but not its expected value.
Strictly speaking, even in the example above we do not really the know standard deviation, but we may have a reliable estimate. Even more important: The knowledge about the standard deviation has been obtained preliminarily, by a procedure that is independent from the random sample we use to estimate the expected value. Nevertheless, in business settings, we typically do not know the standard deviation at all. Hence, we have to settle for sample standard deviation S. Note that, unlike the case in the example above, and S come from the same sample, and we cannot just plug S and replace σ into (9.9). Luckily, we already know that the statistic
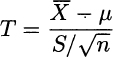
has t distribution with n − 1 degrees of freedom. Hence, if we denote by t1−α/2, n−1 the (1 − α/2)-quantile of the t distribution, using the same procedure described above yields the confidence interval
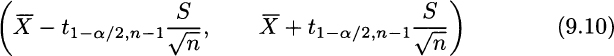
From a qualitative point of view, this confidence interval has the same form as (9.9). The only difference is the use of quantiles t1−α/2, n−1 from the t distribution instead of z1−α/2. From Fig. 7.19 we recall that a t distribution features fatter tails than the standard normal; the fewer the degrees of freedom, the fatter the tails. Hence,
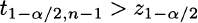
and the bottom line result is a wider confidence interval. This makes sense, since when estimating variance σ2 we add some uncertainty to the overall process; more so, when the sample size n is small.
Example 9.8 Let us consider the random sample:
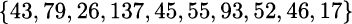
under the assumption that it comes from a normal distribution, and let us compute a 95% confidence interval for the expected value. We first compute the statistics
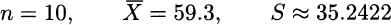
From statistical tables, or a suitable piece of software, we obtain
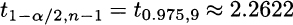
By straightforward application of Eq. (9.10), we obtain the confidence interval (34.0893, 84.5107).
Formula (9.10) is so easy to apply, and it has been implemented in so many software packages, that it is tempting to apply it without much thought. It is also natural to wonder why one should bother to understand where it comes from. The next sections address these issues.
Leave a Reply