An application to finance: value at risk (VaR)

Most financial investments entail some degree of risk. Imagine a bank holding a portfolio of assets; the bank should set aside enough capital to make up for possible losses on the portfolio. To determine how much capital the bank should hold, precise guidelines have been proposed, e.g., by the Basel committee. Risk measures play a central role in such regulations, and a commonly proposed risk measure is value at risk [VaR; please note the capitalization of letters to avoid ambiguity with variance (Var)]. It must be mentioned that bank regulation has been the subject of quite some controversy, in the wake of financial disasters following the subprime mortgage crisis of 2007-2008. In particular, VaR has been criticized as an inadequate risk measure, offering a false sense of security. It has even been suggested that VaR should not be taught at all in business schools.²⁵ However, like it or not, VaR is used; hence, students and practitioners should be fully aware of what it is and what it is not. We will investigate VaR and its limitations further in Section 13.2.3. The first step, however, is understanding VaR in a simple setting.

Informally, VaR allows to say something like

We are X percent sure that we will not lose
more than V dollars over the next N days.

We immediately see that VaR is actually a quantile of the distribution of losses. To clarify the idea, consider a portfolio consisting of a single stock: We own $10 million in Microsoft shares, and we want to estimate one-day VaR, with 99% confidence level. The simplest calculation goes like this: Assume that the daily return of the stock is normally distributed. We know from the square-root rule of Section 7.7.1 that, in such a short timespan, volatility (standard deviation) dominates drift (expected return). Then, assume that daily return is a normal variable with expected value 0% and standard deviation σ_d = 2%. Daily profits and losses can be expressed as the daily variation δW in our wealth:

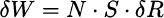
where N is the number of stocks, S their initial price, and δR the random return. We have a loss when δR < 0. If we plot the PDF of profit, losses correspond to the left tail; if we plot the PDF for loss, they are on the right tail; in the case of the normal distribution, given its symmetry, this makes no real difference. To find VaR, we need to solve the equation

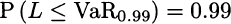
where L = −δW is loss. Given what we have seen repeatedly about quantiles of the normal distribution, we see that we should compute

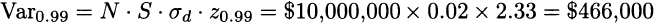
Now what about the 10-day VaR? The following reasoning is often proposed Since volatility scales with the square root of time, it follows that

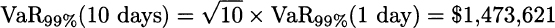
Obviously, this reasoning assumes independence in daily returns, which should certainly not be taken for granted. Furthermore, when we consider time horizons, the drift should not be neglected. More generally, we know that the normal distribution has thin tails and should not be considered a safe model of uncertainty in finance. So, the above calculation should be regarded just as a starting point. Nevertheless, it proves our point: Quantitative concepts can be used (and misused) in a variety of unrelated settings.