The square-root rule

Consider a sequence of i.i.d. random variables observed over time, X_t, t = 1,…, T. Let μ and σ be the expected value and standard deviation of each X_t, respectively. Then, if we consider the sum over the T periods, , we have

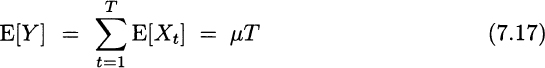
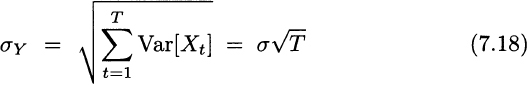
We see that the expected value scales linearly with time, whereas the standard deviation scales with the square root of time. Sometimes students and practitioners are confused by the result concerning standard deviations. It is important to draw the line between the sum of T random variables and the product of T and one random variable.

Example 7.13 Consider demand for an item, over a time interval consisting of T time buckets, say, weeks. The time interval could be delivery lead time, i.e., the time elapsing between the instant at which we issue a replenishment order and the time instant at which we receive the corresponding shipment from the supplier. In practice, demand during lead time is a relevant variable for inventory management decisions. Say that μ and σ are expected value and standard deviation of weekly demand, respectively, and assume that demands in different weeks are independent.

Then, the expected value of demand during lead time is Tμ, but its standard deviation is  and not Tσ. The typical way to get the wrong result is by considering demand during lead time as a random variable

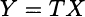
where X is a random variable corresponding to demand during one week. It is true that Var(Y) = T²Var(X), but this is the wrong reasoning; by doing so, we assume that demand during a week is realized, and then it is replicated for T weeks. But this does not correspond to the real phenomenon.

The square-root rule shows that, if T is very small, then the volatility term  dominates the expected value term, as the square root of T goes to zero more slowly than T itself does, when the latter goes to zero. This has some implications for measuring financial risk, as we shall see later, but there is another hidden trap here. It is tempting to apply the rule by considering fractional values of T, but this may lead to nonsense. An example will illustrate the point.

Example 7.14 Let us assume that the yearly demand for an item is normally distributed with expected value 1000 and standard deviation 250. If the lead time is 2 months, what is the distribution of lead time demand D_LT? If we assume that the year consists of 12 identical months of 30 days, and we assume that demands in different months are independent, we could consider the application of the above rules with . In terms of expected value and standard deviation, this would imply

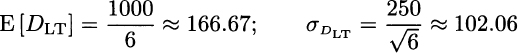
This might make some sense, but can we say that lead time distribution normally distributed? If we recall the three-sigma rule, we note that

In fact, if we assume normality, the probability of negative demand is far from negligible. This example shows that if we assume normality of monthly demand, we may deduce normality of demand during a year, but we cannot go the other way around.