The descriptive statistics, we have introduced concepts like mode, median, and percentiles. We have also remarked that some concepts, in particular the percentiles, are somewhat shaky in the sense that there are slightly different definitions and ways of calculating them using observed data. In this section we examine probabilistic counterparts of these concepts, and how they are related to discrete and continuous random variables.
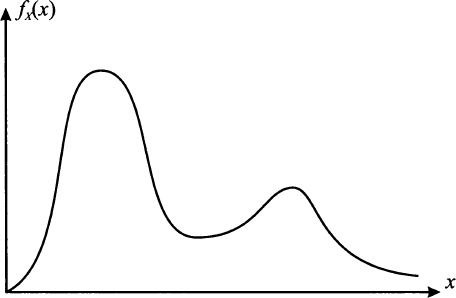
Fig. 7.6 A bimodal PDF
Mode
The mode of a probability distribution is a point at which the PMF or the PDF is maximized. The concept is easy to grasp, but we should point out that the mode for a continuous random variable is not the value with maximum probability, since probabilities of all possible values are just zero. On the contrary, the interpretation for discrete variables is closer to the intuitive concept that we introduced along with descriptive statistics.
The mode need not be unique in principle, as multiple maxima are possible. Most of the theoretical distributions we examine later have a single mode, but, in practice, we may find multimodal distributions in the sense illustrated in Fig. 7.6. We have a well-defined mode, but there is a secondary local maximum. If the distribution is built by fitting against empirical data, it may be the case that the secondary mode is just sampling noise. However, we should never discard the possibility that we really need a sort of mixed distribution to model different dynamics of a phenomenon.
Leave a Reply