Consider a stylized economy with three possible future states of the world, as illustrated in Fig. 3.9. Say that three securities are available and traded on financial markets, with the following state-contingent payoffs:
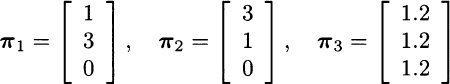
These vectors indicate, e.g., that asset 1 has a payoff 1 if state 1 occurs, a payoff 2 if state 2 occurs, and a payoff 0 in the unfortunate case of state 3. We may notice that the third security is risk-free, whereas state three is bad for the holder of the first and the second security. Let us also assume that the three securities have the following prices now: p1 = p2 = p3 = 1. What should be the price of an insurance against the occurrence of the bad state, i.e., a security paying off 1 if state 3 occurs, and nothing otherwise?
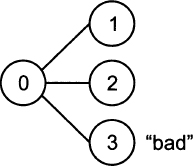
Fig. 3.9 A three-state economy: insuring the “bad” state.
Following the ideas that we have already applied in binomial option pricing, we can try to replicate the payoff of the insurance by a portfolio consisting of an amount αi of each security, for i = 1, 2, 3. Finding the right portfolio requires finding weights such that the payoff vector of the insurance is a linear combination of payoffs πi:
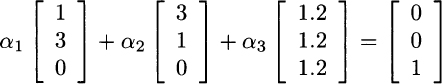
This is just a system of three equations in three unknown variables and yields:
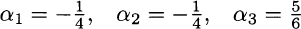
Note that we should sell the two risky securities short. But then, invoking the law of one price, in order to avoid arbitrage opportunities, we may find the fair price of the insurance:
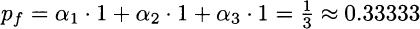
In this case, we are able to price a contingent claim because there is a unique solution to a system of linear equations. In fact, given those three priced assets, we can price by replication any contingent claim, defined on the three future states of the world. In financial economics, it is said that the market is complete.
However, if we enlarge the model of uncertainty to four states, we should not expect to price any contingent claim as we did, using just three “basic” securities. Furthermore, assume that we have three traded securities with the following payoffs:
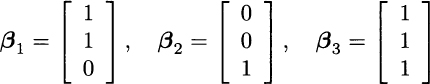
We immediately see that β3 = β1 + β2. The third security is just a linear combination of the other two and is, in a sense that we will make precise shortly, dependent on them. If we take linear combinations of these three securities, we will not really generate the whole space ![]() :
:

We see that, on the basis of these three assets, we cannot generate a security with two different payoffs in states 1 and 2.
Generalizing a bit, when we take a linear combination of vectors and we set weights in any way that we can, we will span a set of vectors; however, the spanned set need not be the whole space ![]() .
.
Leave a Reply