In this section we try to further motivate the use of definite integral, at least conceptually, for business management problems. To do so, we use the EOQ model of Section 2.1 once again. There, we have claimed that the contribution of inventory holding cost to average total cost per unit time is
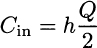
In the reasoning, a key role is played by the fact that demand rate is constant, and given by D items per unit time.29 But what can we do if demand rate is an arbitrary function D(t) of time? The holding cost, in such a case, depends on the ordering policy we follow, as well as on the initial inventory level.30 Whatever we do, it will result in a time-varying on-hand inventory level that we may represent by a function I(t). Then, the holding cost of our ordering policy, over time interval [0, T] is just
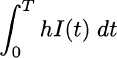
To see this, think of an inventory level I(t) that varies in time; since time is continuous, we should take the instantaneous inventory level I(t) along the time interval, multiply it by the unit inventory holding cost h, and “sum” the results. In this case, the sum is actually an integral, which informally is the sum of infinite tiny, infinitesimal terms.
To see that this works for the EOQ model, consider the first triangle in Fig. 2.1. This corresponds to the first ordering cycle. We start with I(0) = Q, and after an interval corresponding to the time between two consecutive orders, T = Q/D, we have I(T) = 0. On that interval, inventory as a function of time is given by
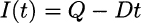
The inventory cost on this cycle is
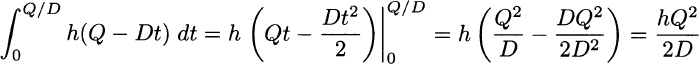
This expression is just h times the area of a triangle with base Q/D and height Q. Since there are D/Q such cycles per unit time, on average, the average holding cost is:
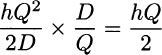
as we claimed before.
Thus, integrals can be used when we have to model complicated business problems where variables of interest change in continuous time. In general, building and/or solving such a model is difficult, and one resorts to time discretization. The idea is to partition time interval [0, T] into n subintervals of width Δt, as we did in Fig. 2.32. Then, we have n time buckets of the form [(i − 1) Δt, i Δt], for i = 1, …, n. If we denote the inventory level at the end of ith time bucket by Ii = I(i Δt), we can approximate the total holding cost as
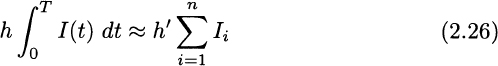
where h′ ≡ h Δt is the unit holding cost for a time period of length Δt. This expression can be definitely more manageable when building possibly large-scale decision models.31
A possible objection is that we should take the average inventory level rather than the inventory level at the end of a time bucket. Doing so results in the following expression:
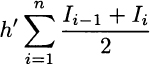
This may look quite different from (2.26), indeed. However, in practice the two expressions are equivalent. To see this, let us expand the sum:
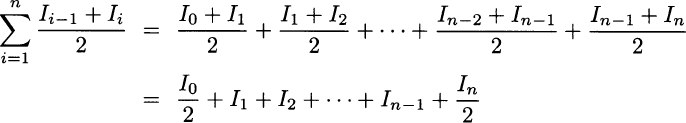
Comparing this against (2.26), we see a difference in the first and last terms. However, the first term is a constant, as the initial inventory level is given and it is not a decision variable. The last term, if it is not fixed to a positive value, will be set to zero by the optimization algorithm; in fact, the holding cost is minimized, and since the model does not see any demand beyond the last time bucket, there is no reason to have any item left in inventory. To avoid running out of stock at the end of the planning horizon, we should assign a value to the terminal inventory level; but then, the last term is a constant just like the first one. So, we see that considering the inventory level at the end of each time bucket is equivalent to considering the average inventory level. Coincidentally, this is consistent with the finite sums we have considered in Section 2.13.1.32 The choice between a continuous-time and a discrete-time model is largely a matter of convenience, depending on the business problem at hand.
Problems
2.1 Find the domain of functions
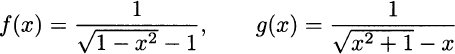
2.2 Find the equation of a line
- With slope −3 and intercept 10
- With slope 5 and passing through point (−2, 4)
- Passing through points (1, 3) and (3,−5)
2.3 Find the first-order derivative of the following functions:
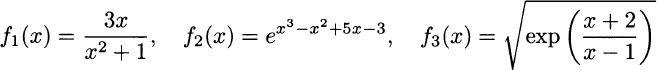
2.4 Consider functions f(x) = x3 − x and g(x) = x3 + x. Use derivatives to sketch the function graphs, and look for maxima and minima.
2.5 Consider the following functions defined on piecewise domains:
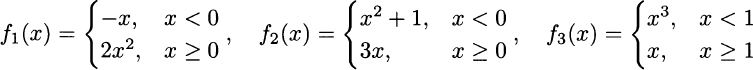
For each function, indicate whether it is continuous and differentiable at the point of transition between each portion of the domain.
2.6 Consider function
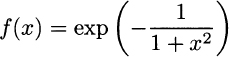
and find linear (first-order) and quadratic (second-order) approximations around points x0 = 0 and x0 = 10. Check the quality of approximations around these points.
2.7 In Example 2.33 we assume discrete-time compounding of interest. This results in the need for introducing modified duration, in Eq. (2.19), to get rid of an annoying factor 1 + y, where y is yield to maturity. Compute bond duration when assuming continuous-time compounding, at yield yc, and show that this correction is not necessary in this case.
2.8 Consider the following functions and tell if they are convex, concave, or neither:
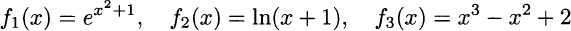
2.9 Prove that the intersection of two convex sets S1 and S2 is a convex set.
2.10 Consider a stream of constant cash flows Ft = C, for t = 1, …, T. From Example 2.39, we know how to find its present value at time t = 0. Now imagine that these cash flows are the amount you invest to build your pension wealth; the current amount of wealth is invested at an interest rate r, which we assume fixed and constant over time. How can you compute your future pension wealth at time T?
2.11 Assume that you work from age 25 to age 65. At the end of each year, you contribute C to your pension fund, which is invested at a yearly rate r = 5%. At age 65 you retire and plan to consume $20,000 each year, until you die. Assuming that you die at age 85, and that interest rates remain constant, how much should you save each year? How does the result change if, due to your reckless lifestyle, you assume that departure will occur at age 75? (Hint: Use Problem 2.10.)
2.12 Consider the following extension of the EOQ model, often labeled economic manufacturing quantity (EMQ). Most of the assumptions of the EOQ and EMQ models are the same, but in the latter, rather than assuming instantaneous replenishment of inventory, inventory is replenished at production rate p, which gives the number of parts produced per unit time. Find the order quantity minimizing the sum of inventory and ordering cost, averaged over time. (Hint: Draw the inventory level during an ordering cycle.)
Leave a Reply