Motivation: definite integrals as an area

Consider a function f on interval [a, b]. If the function assumes nonnegative values on that interval, it will define a region below its graph; this is illustrated as the shaded region in Fig. 2.31. Now imagine that we are interested in the area of that region. If the function were constant or linear, we would get the result by recalling a few concepts from elementary geometry. In the case of a constant function, we would just compute the area of a rectangle, and the area of a trapeze is needed for a linear function; but if the function is arbitrary, things are not that simple. Nevertheless, we could try to find a suitable approximation of the area. Since we know pretty well how to cope with a constant function, we could try to approximate f by a piecewise constant function. The idea is illustrated in Fig. 2.32. More precisely, we can partition the interval [a, b] into n “slices” of width

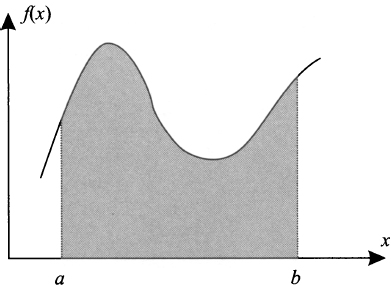
Fig. 2.31 The area below a function graph.

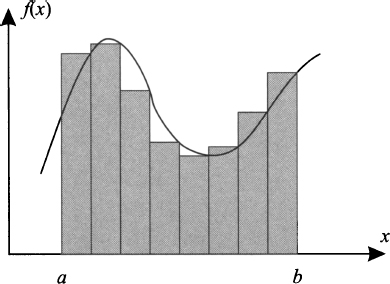
Fig. 2.32 Approximating area by piecewise constant functions.

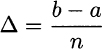
Each slice is a subinterval with extreme points of the form

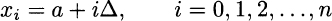
Note that x₀ ≡ a and x_n ≡ b. The first subinterval is [x₀, x₁] ≡ [a, a + Δ], and in general we have subintervals like [x_i−1, x_i], for i = 1, …, n. Then, we should decide how to assign the height of each rectangle in Fig. 2.32. The choice in the figure is to consider f(x_i), i.e., the value of the function on the right endpoint of each subinterval [x_i−1, x_i], but different choices could make sense as well. With our approximation, the area is

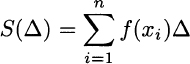
where the notation highlights the dependence of sum S on the selected subinterval width Δ. Reasonably, the smaller this width, the better our approximation, and (maybe) taking a very fine partition with a very small Δ, we would really find the area we need. This results in the following (informal) definition of the definite integral of function f on interval [a, b]:

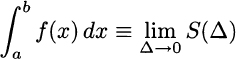
The notation ∫ looks a bit like a slanted S; indeed, this reminds us that the integral is basically the limit of a sum. By the same token, the notation dx refers to an infinitesimal increment in the x variable; the notation Δx or δx is used when referring to small but finite increments.

Our treatment leaves a lot to be desired, to say the least, as we should clarify under which conditions the sum will converge to a limit. Furthermore, one could wonder whether our choice of rectangles is the best one or if it really makes any sense. Indeed, a rigorous treatment of integral should follow a slightly different route. Nevertheless, this is the simplest way to grasp the essential concept of an integral. Incidentally, if the function takes negative values on some subintervals, we can just consider the associated area as a negative one, which can be summed algebraically to positive areas.