If the derivative of function f at point Xo exists, then we say that the function is differentiable at point x0; if this holds for all points on an interval or domain, the function is differentiable on that interval or domain. If the derivative f′(x) exists at all points x on an interval and the derivative is a continuous function, we say that the function is continously differentiable on that interval.
In Section 2.4 we have encountered discontinuous functions. If a function f is discontinuous at x0, then
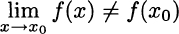
We have also noted that a limit should not depend on the way x approaches x0; the limit, if it exists, must be the same for 
(from the right) and 
(from the left). Since the derivative is defined as a limit, we may have similar concerns. To see a couple of standard cases in which the derivative does not exist, have a look at Fig. 2.19. Graph (a) shows a typical “kinky” function. This function is actually a piecewise linear function, and for most points the derivative is just the slope of the corresponding linear piece. But where the two lines join, we have a point of nondifferentiability: the left and the right limit are different, and all we have are a left derivative and a right derivative.
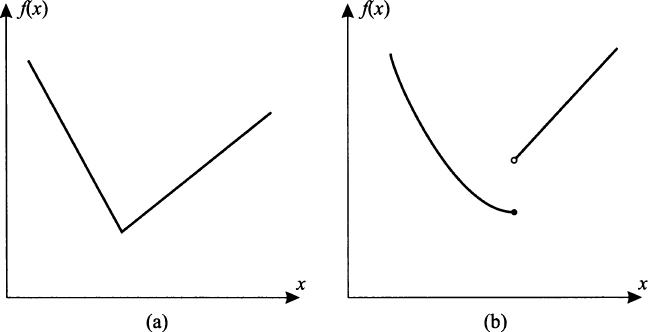
Fig. 2.19 The derivative may fail to exist.
Example 2.17 The absolute value is a function defined as
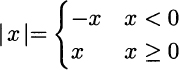
The derivative of this function is
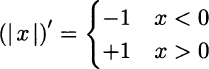
At point x = 0 we do not have a derivative since
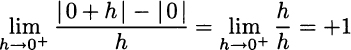
whereas
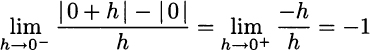
The two limits above are different and do not define a derivative, but only a right derivative and a left derivative, respectively. We may also observe that there is no well-defined tangent line at the kinky point.
Figure 2.19(b) shows a typical discontinuous function. It is also clear that we do not have a well-defined derivative where a function jumps.
Putting the two graphs together, we notice an interesting fact. If the function jumps, i.e., is discontinuous, we fail to find the derivative. However, even if the function is continuous, we may fail to find the derivative. Indeed, the kinky function in Fig. 2.19(a) is a continuous function. This suggests that continuity is a necessary condition for differentiability, but not a sufficient one. In other words, if the function is differentiable, then it must be continuous, but not vice versa. To see this, consider this equivalent definition of derivative
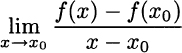
If this limit exists, it must be the case that, for x → x0, the numerator gets closer and closer to zero:
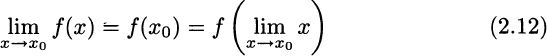
Note that, for a continuous function, the limit of the function is the same as the function of the limit.
It is tempting to think that, after all, such weird functions are the result of mathematical phantasy, nowhere to be found in the real world. The following example shows that this is not the case.
Example 2.18 (All-unit and incremental discounts) Quite often, when purchasing a product, we are offered price discounts, provided we buy a number of items exceeding a given breakpoint. For instance, the unit price could be €10 per piece, but if we buy at least 100, the unit price drops to €9. Actually, there are two different cases:
- In all-unit discounts, the discounted price applies to all of the units we buy.
- In incremental discounts, the discounted price applies only to items beyond the breakpoint.
Let us write down the total cost function C(x) depending on the purchased amount x, assuming for simplicity that x is a real number, which is sensible for items bought in units of weight or volume and is a fair approximation for discrete items bought in large quantities. The cost for all-unit discount is
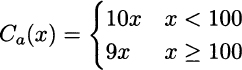
whereas cost for incremental discount is
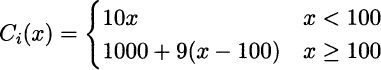
Qualitative sketches of the two functions are illustrated in Fig. 2.20. Graph (a) shows a weird feature of all-unit discount: Close to the price breakpoint, we pay less if we buy more. Disregarding this issue, we see how discontinuous or nondifferentiable functions may actually arise in practice. As another example, think of the different tax brackets as a function of income. The plot of the tax amount we have to pay would be similar to the incremental discount case, but when dealing with taxes, the slopes of the linear pieces are increasing rather than decreasing.
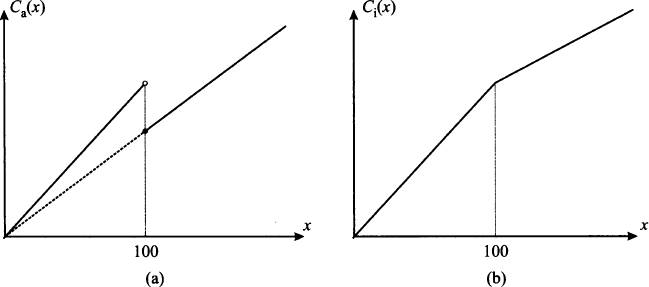
Fig. 2.20 Nondifferentiable functions arising from discount opportunities in purchasing decisions.
Leave a Reply