The next step is to consider powers of the independent variable x. A term of the form axm is called a monomial of degree m. Summing monomials, we get a polynomial function:
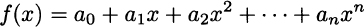
Here n is the degree of the polynomial. A few polynomial functions are shown in Fig. 2.8. A quick glance at the three plots suggests a few observations:
- The first polynomial function is always increasing and does not have a point minimizing or maximizing its value (the maximum goes to +∞ and the minimum goes to −∞).
- The second one has a point that is both a local and a global minimum; that point is where the function stops decreasing and starts increasing.
- The third one has two local minima, one of which is also the global one, as well as a local maximum.
We define concepts like local or global minimum later, but the intuition should be clear from the figure. Informally, a local minimum is a point such that we see an increase in the function while moving both to its right and to its left, but it need not be the true globally minimum of the function, as the function could take a lower value somewhere else.
While a linear function is either increasing or decreasing over the whole real line, a polynomial function may oscillate. In general, the larger the degree of a polynomial, the larger the possibility for up/downswings. As a consequence, a polynomial may have several roots, i.e., solutions of the equation f(x) = 0. In Fig. 2.8, the graph of the last polynomial crosses the horizontal axis a few times, while a linear function does so exactly once (unless it is a constant function). The number of roots is impossible to determine for a generic function, but a polynomial of degree n may have up to n (real) roots.
Leave a Reply