There are very few real-world systems that behave like the simplified mathematical model we used above for a particle in a box. However, recent developments in the nascent field of nanotechnology have made it possible to produce nanostructures of only 2–10 nm in size that exhibit behavior close to the simple particle-in-a-box model we discussed.
These tiny structures are known as quantum dots. As shown in Figure 111, they are small semiconductor crystals of only 10 to 50 times the diameter of an atom. A semiconductor is a material in which an electric current can flow due to the movement of electrons and “holes”—states where electrons could sit, but which are empty and thus act as positive charge carriers. You can study about those in most introductory books on electronics. For our purposes, it is sufficient to say that the quantum dots contain free pairs of one electron and one “hole” that can move freely inside the semiconductor, but cannot get out—just like in the quantum particle-in-a-box problem. Quantum dots of different dimensions are currently being manufactured using semiconductor materials such as cadmium selenide/zinc sulfide [CdSe/ZnS] and indium phosphide/zinc sulfide [InP/ZnS].
Figure 111 Quantum dots are nanometer-sized crystals in which electrons and “holes” get trapped, acting as real-world models of the particle-in-a-box problem. (a) The quantum dots are made of semiconductor materials such as InP/ZnS, in which the size of the dot can be controlled very well at the time of manufacture. (b) An organized array of atoms is seen in this TEM image of a 10-nm quantum dot.
Do-it-yourself synthesis of quantum dots is possible, and relatively simple procedures using equipment available in undergraduate laboratories have been published,34,35 but they involve the use of rather toxic materials which we prefer to avoid. Instead, we purchased a set of four vials, each containing a suspension of quantum dots of a specific radius (2.37, 2.53, 2.72, and 2.92 nm). The quantum dots consist of indium phosphide cores surrounded by thin zinc sulfide shells. They are made by Nanosys for Cenco Physics, and are available from educational scientific supplies stores such as Sargent Welch (catalog number WLS1751-18). Another source of ready-made nanocrystal quantum dots is Evident Technologies. They sell kits containing a number of small (although somewhat expensive) vials of CdSe/ZnS and lead sulfide (PbS) quantum dots.
As shown in Figure 112, a quantum particle trapped in a box can absorb a photon (or be excited in some other way), causing the system to move to a higher energy state. However, the higher energy state is unstable, and will eventually decay to the ground state by emitting a photon with energy Ephoton = hf = ΔE. Similarly, when a quantum dot is illuminated by a photon of sufficiently high energy, an excited electron-hole pair forms inside the quantum dot. When the electron and hole recombine, the quantum dot returns to its ground state, and a photon is emitted with a wavelength dependent on the radius of the quantum dot. Smaller dots emit photons with shorter wavelengths.
Figure 112 A quantum particle in a box can move to a higher energy state when it absorbs a photon of sufficient energy (a), (b) The excited state is not stable, so the system will tend to return to its ground state by emitting a photon with energy equal to the difference in energy between the two states.
Before we experiment with real quantum dots, we must modify the equations to accommodate the fact that the quantum dots are not one-dimensional “boxes,” but instead have a spherical geometry. We must also account for the presence of two particles within the box (an electron-hole pair), and consider that the box is not empty, but rather filled with a semiconductor material (which increases the ground state by 2.15 × 10−19 J). We won’t go into the derivation of the equation for the InP/ZnS quantum dot, but instead limit ourselves to stating that the energy of the fluorescence (emitted) photon is:
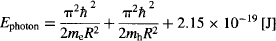
where
R = radius of the quantum dot
me = effective mass of the electron inside the semiconductor = 7.29 × 10−32 kg
mh = effective mass of the hole inside the semiconductor = 5.47 × 10−31 kg
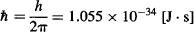
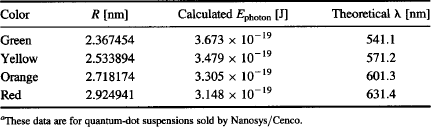
To conduct an experiment, illuminate a quantum-dot suspension with a UV LED (at a wavelength of approximately 405 nm) as shown in Figure 113a. Use the spectrometer that you built (Figure 80) to photograph the spectrum of the light emitted by each quantum-dot suspension. Process the photographed spectra using VisualSpec to obtain spectral plots similar to those of Figure 113b. What is the peak wavelength you measure for each quantum-dot size? How well do your measurements match the theoretical peak emission (Table 6)? Plot the quantum-dot radius versus the peak emission. What type of relationship does this graph show?
Figure 113 Suspensions of quantum-dot nanocrystals illuminated with UV light behave very similarly to a theoretical quantum particle in a box (a), (b) The fluorescence spectra from various quantum-dot suspensions agree with Schrödinger’s equation for the quantum particle in a box if adjustments are made to account for the presence of two particles within the box (an electron-hole pair), and for the fact that the “box” is filled with a semiconductor material.
TABLE 6 Nanocrystal Radii and Calculated Fluorescence Wavelength for Quantum-Dot Suspensionsa
Leave a Reply