Introduction

We learned that |Ψ|²—the square of a system’s wavefunction—is itself a function that gives us the probability of finding a particle at a certain time and position. However, in the simply assigned the fancy symbol |Ψ|² to the probability of finding a particle at a certain place and at a certain time. For example, in the simple case of the double-slit experiment of Figure 101, we just gave the distribution of electron hits on the screen of Tonomura’s electron microscope the name |Ψ|², but we didn’t calculate what |Ψ|² would look like before we looked at the results of the experiment.

In 1925, Austrian physicist Erwin Schrödinger figured out a way of calculating the wavefunction of a system, allowing the behavior of an experimental system to be predicted.

Possibly, the simplest problem that we can solve using Schrödinger’s equation is the so-called “particle-in-a-box” problem, in which we determine the probability of finding a particle at a certain position within an ideal box. As shown in Figure 109, a particle of mass m is trapped between two infinitely high walls. Let’s assume the box is in the vacuum of space, away from gravitational pull and any other influence. The walls are perfectly elastic, so they don’t absorb any energy from the particle. This is modeled by setting the potential energy at zero between the two walls, and making it infinite outside the box:

Figure 109 In the particle-in-a-box problem, one attempts to calculate the position of the particle within a box lined by two perfectly elastic, impenetrable walls. (a) A classical particle simply bounces back and forth between the walls at a speed related to the particle’s energy. (b) The position of a quantum particle is unknown until measured, but the probability of finding the particle possessing a certain amount of energy can be calculated with Schrödinger’s equation.

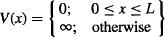
Mathematically, since the total energy of the particle is given by the sum of its potential and kinetic energies, the particle would need an infinite amount of energy to be outside the box (where V = ∞). As such, the particle must be located somewhere between x = 0 and x = L.

In the classical case of Figure 109a, the particle simply bounces back and forth between the walls at x = 0 and x = L with velocity v. Since the box has perfectly reflecting boundaries, every time the particle hits the wall, its velocity is reversed from v to –v. If we know the particle’s position and momentum at any moment, we can calculate the particle’s future position at any time using Newton’s equations.

The classical momentum and energy of this particle are:

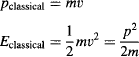
The particle is allowed to have any nonnegative, noninfinite energy, including zero—in which case it would simply rest at a certain position forever. The important point is that the position and velocity of this classical particle are determined at every instant, regardless of whether it is being observed or not.

For a very small particle however, Heisenberg’s Uncertainty Principle will become very significant, and we will not be able to simultaneously know the precise position and precise momentum of the particle at any time. Just like an electron in Bohr’s atom, a particle in the one-dimensional box of Figure 109b is in a bound state with a definite energy, but it has no definite position, because of the Uncertainty Principle. As such, the quantum particle within the box has a definite momentum (and hence has definite energy), but its position inside the box is completely random. When it is not observed, the quantum particle exists in a random state, which in quantum physics is called a virtual state, whereby the position of the particle—if measured—could be anywhere within the interval 0 ≤ x ≤ L. We know that if we run the experiment many times we will find a probability distribution that we have called |Ψ|².

Schrödinger’s achievement was to come up with a differential equation to calculate Ψ just from a mathematical definition of the problem. Don’t panic if you don’t yet know (or no longer remember) calculus! We work with the solutions to the equations. In spite of this, let’s take a look at Schrödinger’s equation for a simple, one-dimensional system that doesn’t vary with time. Conveniently, our one-dimensional particle in a box is just this type of simple system. Ready? Here it goes:

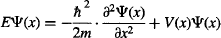
Breathe deep. Don’t panic. In this equation:

Ψ(x) is the particle’s wavefunction as a function of x

E is the energy of the system

m is the mass of the particle

V(x) is the potential experienced by the particle as a function of x, and

 is Dirac’s constant, which as you may remember is .

The ∂²Ψ(x)/∂x² part is the second derivative of the wavefunction Ψ(x), which is a complicated way of saying that it is a mathematical operation that describes how Ψ(x) changes from one place to another. Don’t worry about it, we’ll calculate it for you in case your calculus is not up to speed.

Now, we know the following two things that really simplify Schrödinger’s equation for our simple particle-in-a-box problem:

1. The particle cannot be outside the box, so Ψ = 0 for x ≤ 0 and x ≥ L.

2. The potential V(x) experienced by the particle within the box is zero.

So, we can get rid of V(x)Ψ(x), leaving us with:

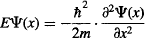
The solution to this differential equation is:

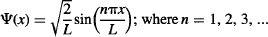
Notice that the wavefunction is dependent on a sine function, so it will work out for integer multiples of πx/L, which is why there are multiple wavefunctions for this system that depend on n. As you may realize by now, the reason for multiple solutions at integer values comes from quantization of energy. That is, the trapped particle is allowed to have only discrete levels of energy given by:

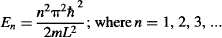
Notice that n cannot be zero. This is very interesting, because it means that while a classical particle trapped inside a classical box can sit motionless (have zero energy), a quantum particle cannot have zero energy. How is that possible? Well, if the quantum particle would sit motionless, then we would know its exact position. However, according to Heisenberg’s Uncertainty Principle, this would mean the particle must have infinite momentum, which is impossible, since the particle is sitting motionless. The opposite idea doesn’t work either, since if we say that the particle has zero momentum, we can’t know anything at all about its position. However, we know that the particle is somewhere within the finite box, making it impossible for it to have zero momentum…

The state of the system for n = 1 is known as its ground state, and the amount of energy that the system has in this state is known as the zero-point energy. This very unintuitive and absolutely fascinating consequence of quantum physics appears with even the simplest quantum system. By the way, you need to be very careful about claims made about devices that supposedly extract useful energy out of the zero-point energy. No device claiming to operate using zero-point energy has ever delivered on its promise.

Let’s return to the energy levels that result from Schrödinger’s equation:

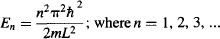
For n = 1, the ground state energy is:

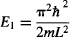
and the energy for all other levels is found by multiplying the zero-point energy by n²:

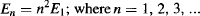
where n is known as the system’s quantum number.

Another interesting result from the solution of Schrödinger’s equation is that the probability of finding the quantum particle within the box is variable. As shown in Figure 110, classical physics predicts that the probability of finding the particle at any point within the box is equally distributed over the box. Classical probability within the box is simply a line at 1/L. On the other hand, the quantum probability is not only unevenly distributed, but there are points within the box where the particle could never be found! This might not be too surprising, until you think about how that particle gets from one side of the zero to the other side of the zero. The Copenhagen Interpretation avoids this problem by telling us this is a question that cannot be asked, since “what cannot be observed does not exist.”

Figure 110 There is a very large difference between the predictions made by classical and quantum physics for the position at which a particle is found in a one-dimensional box. Quantum physics even predicts that there are points at which the particle will never be found inside the box.