Experimental confirmation of de Broglie’s formula came in 1927, when G. P. Thomson at the University of Aberdeen and C. J. Davisson with L. H. Germer at Bell Labs observed diffraction—a typical wave-like behavior—from an electron beam.
Unlike photons, electrons have a rest mass, and are thus perceived as “solid” particles. Electrons are negatively charged and can be accelerated with ease, as is commonly done inside a CRT. Let’s suppose that electrons, which have a mass of m = 9.1 × 10−31 kg and charge of e = 1.60 × 10−19 Coulomb are fired by an electron gun operated at a potential of V = 4 kV (Figure 95a). Their kinetic energy is:
Figure 95 Electron diffraction can be observed in the laboratory with a specialized CRT. (a) Simplified representation of a vacuum tube used to observe the wave-like nature of electrons. (b) Simplified view of diffraction of electrons by a crystal.
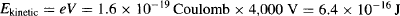
Since
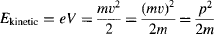
the momentum of these electrons accelerated at 4 kV is thus:
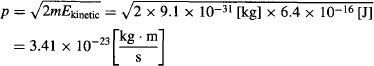
which according to de Broglie gives them a wavelength of:

De Broglie’s hypothesis would prove correct if one could shoot electrons at a double slit and obtain an interference pattern.
Let’s see how we could do that in the lab. Look at Figure 95a, and remember that when we experimented with microwave two-slit interference (Figure 18), we found that fringes appear at angles that satisfy s(sin θ) = λ. This formula also applies to simple ruled diffraction gratings, where the condition for diffraction is λ = s(sin θ), or θ = λ/s for small angles. Since the experiment has to be carried out in a vacuum tube, we could assume a 10-cm-diameter bulb. Therefore, the grating spacing between rulers to produce interference at 1 cm would be:
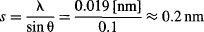
Although producing an artificial grating with rulings of approximately s = 0.2 nm is no easy task, the lattice of crystals can act as natural “gratings.” Graphite was used by the Bell Labs team in 1927 to observe electron diffraction. And for a very good reason—a piece of graphite can be assumed to have its carbon atoms organized in a simple cubic lattice with the right spacing: 1 mol of carbon atoms (remember Avogadro’s number = 6.022 × 1023?) weighs 12 g, and since the density of carbon is approximately 2 g/cm3, 1 cm3 contains ~ 1023 atoms spaced 0.215 nm apart.
Davisson and Germer fired an electron beam at a thin graphite crystal, and observed that the beam was diffracted according to the angles given by the formula usually used for the diffraction of light (Figure 95b):
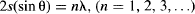
This clearly showed that de Broglie was right. It’s not only that light sometimes acts as particles, but particles with mass sometimes act as waves. Particle–wave duality seems to be a universal characteristic of everything that exists. The 1929 Nobel Prize in Physics was awarded to Louis de Broglie “for his discovery of the wave nature of electrons.”
There are a number of commercially available tubes that are specifically made for the didactic demonstration of electron diffraction. They are made by Leybold (model 555626), PHYWE Systeme (model 06721.00), and Teltron (models 555 and 2555). We purchased one of the Teltron 555 tubes on eBay for around $100 (a new 2555 sold by Tel-Atomic is over $850) and hooked it up as shown in the diagram of Figure 96a. The source of electrons in the 555 tube is an indirectly heated cathode. The heater is a filament that needs to be supplied from a 6.3-V transformer designed specifically to supply vacuum tube filaments, for example a model 166F6 by Hammond Manufacturing. Once the cathode temperature has been allowed to stabilize, the voltage between the cathode and the anode is increased, so electrons are focused and accelerated by the cylindrical portion of the anode. A micro-mesh nickel grid coated with graphite is the target for the converging beam of electrons. The graphite coat is only a few molecular layers thick and can easily be damaged by a current overload. For this reason, the anode current should be monitored and never allowed to exceed 200 μA. An internal resistor biases the cathode, but an external 0–50 VDC power supply is used to focus the beam of electrons, which sharpens the diffraction pattern and allows better observation, especially at lower cathode-to-anode voltages.
Figure 96 Geometry to interpret the diffraction-tube results. (a) Connection of Teltron model 555 electron-diffraction tube. (b) Graphite has a hexagonal crystal lattice structure, in which the planes on the right are responsible for the first two rings of the diffraction pattern. (c) The diameter of the rings depend on the diffraction angle and geometry of the tube.
If graphite had a simple cubical structure, we would expect to see four spots on the screen. As shown in Figure 96b, however, graphite has a hexagonal structure; because of this sixfold symmetry, it should yield six spots on the screen for s1 and six for s2. Each of the six spots for each s should cause the same amount of diffraction but should rotate about the direct beam, each separated by 60°. However, the hexagonal structure is made of planes of hexagonal rings only loosely bonded to each other, resulting in many minicrystal planes randomly oriented to one other. The resulting first-order diffraction pattern from this randomly oriented powdery crystal is thus made of two rings, one for each spacing s.
As shown in Figure 96c, two prominent rings are observed on the screen at a voltage of 4 kV. For simple diffraction, the condition is λ = s(sin θ), which for small angles may be simplified as λ = sθ. The Teltron 555 tube has a target-to-screen distance r of 14 cm, so the expected diameters for the circles can be calculated as:
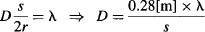
Measured diffraction ring diameters need to be compensated for the curvature (66 mm) and thickness (1.5 mm) of the 555 tube. When this is done, and the voltage is varied between 2.5 and 5 kV, one can see that the tube produces diffraction ring diameters that accurately match the predictions made by de Broglie’s hypothesis.
Build one of these setups and try it out yourself! This should be a deeply moving experience if you understand its implication: a particle of matter is not a “solid ball” but can behave as an ethereal wave!
Leave a Reply