Let’s see those hydrogen lines for ourselves!
We will use the kind of hydrogen “spectrum tube” available at any store that sells educational scientific supplies. Although they are all pretty much the same, their price varies quite a bit based on the store’s brand name. The least-expensive spectrum tubes are sold by Information Unlimited (under $20). You can buy these filled with different gases, such as hydrogen, oxygen, nitrogen, neon, argon, and helium. They are made specifically to study the emission spectra of pure elements, so their internal pressure, electrode materials, and dimensions have been optimized to produce sufficient intensity for spectral analysis. These tubes are not designed to be used as decorative lamps, and should not be operated for longer than 30 seconds before they are switched off for at least another 30 seconds. You can energize these tubes from the power supply shown in Figure 78. The high-voltage module we used is sold by Information Unlimited as model NEON21, but the high-voltage AC power supply of Figure 39a (without the voltage multiplier of Figure 39b) works just as well. Please note that it is usually enough to connect only the high-voltage AC terminal from a high-frequency power supply to one of the tube ends, leaving the other tube end floating. If this works with your power supply, it will prolong the tube’s life.
Figure 78 We built this simple high-voltage power supply to energize commercial spectrum tubes. R3 and R6 should be trimmed to power the tube for only 30 s before it is turned off and allowed to cool down for 30 s. We built a plastic stand for the tube and used clips from a 1/2-in.-diameter fuse holder to connect the power supply to the tube.
After you experiment with the purpose-made tubes, try building your own spectrum tubes using the simple glow-discharge tube (Figure 42) by back-filling the tube with some hydrogen, helium, or other gases to which you may have easy access. For example, you could produce hydrogen by electrolysis of water, use helium from a party balloon, or obtain argon from a welding supplies store. However, don’t expect the spectral purity of commercial spectrum tubes unless you have a system that can pull a very deep vacuum and use laboratory-grade gases. This is because your system at a rough vacuum will still contain quite a bit of air (which is mostly nitrogen), water vapor, and by-products of the vacuum oil.
The other item that we need to observe hydrogen’s emission lines is a spectrometer or spectroscope.* We built one using a prism back to study the blackbody radiation spectrum (Figure 21). However, one that is more portable and easy to use can be made from a grooved piece of plastic film known as a diffraction grating. The fine periodic grooves in the grating diffract light at an angle that is dependent on wavelength. For example, take any compact disk or DVD, and shine a light on its surface. The very fine grooves arranged in a spiral act as a grating and disperse the light into its constituent components, because each wavelength that is part of the illuminating white light is sent into a different direction, producing a rainbow of colors under white light illumination. The end result is similar to the operation of a prism, although the optical mechanism is very different.
There are many plans on the Web for building a spectroscope with a CD acting as a reflection diffraction grating. However, we recommend that you use a transmission diffraction grating slide for making your spectroscope. These are available from educational science supply stores and many other online sources, often for under $1. Chose a linear diffraction grating with 1,000 lines/mm that is mounted on a 35-mm slide. Alternatively, you may purchase a ready-made, inexpensive student spectroscope with a calibrated wavelength scale, preferably the Project STAR spectrometer manufactured by Science First.
To make your own spectroscope, find or make a cardboard box for the body of your instrument. An empty cereal box works very well. Carefully take the box apart and paint the inside flat black. Once it dries completely, cut a rectangular hole for the diffraction grating slide, as shown in Figure 79. Cut a very narrow slot directly across the slide. The slot should be around 0.5-mm wide and 3-cm tall. If it’s easier for you, cut a wider slot (e.g., 1 cm) and use two index cards over the slot to form the narrow slit. Place a single strip of translucent adhesive tape (e.g., Scotch Matte Finish Magic Tape) over the slit.
Figure 79 You can build a simple, but very useful, spectroscope using a diffraction grating slide. The spectroscope is shown with the top cover removed for clarity. Make the housing out of a cardboard box the size of a cereal box. Cut a narrow entrance slit to produce a very sharp spectrum. Print a calibrated scale on a piece of translucent plastic above the spectrum so that you can explore sources with unknown spectra.
Next, temporarily reassemble the box with the exception of the top cover. Tape the diffraction grating slide in place, and look at a light source. Mark the area where you see the spectrum, and cut a 1-cm high slot over that area. Tape a piece of translucent plastic (we used a strip of plastic that we cut out of a milk jug) over the slot that you just cut. This is where you will print your wavelength scale. Now, observe a number of sources with known emission spectra and mark the scale accordingly. Lastly, tape the top of the box and start exploring!
Observe various sources of light that are used for everyday illumination. What do you notice about the spectrum produced by an incandescent lightbulb, a fluorescent lightbulb, and a street lamp? By now you should be able to tell why the incandescent lightbulb behaves as a blackbody and produces a continuous spectrum. But how about the fluorescent light? Why does it look white to you despite its spectrum consisting of discrete lines?
Adding an inexpensive digital camera to the spectroscope allows the “rainbow” spectra to be analyzed by a computer to produce quantitative spectral plots. As shown in Figure 80, we built a wooden base to hold our Project STAR spectrometer and an old digital camera. We used a rubber grommet to couple the spectrometer’s eyepiece to the camera’s lens. We taped a piece of electroluminescent (EL) foil in front of the scale slot so that we would always get our pictures to include an evenly illuminated scale. We mounted the inverter for the EL lamp and a 9-V battery under the plywood base. We used some EL foil that can be cut to the desired shape with scissors. These EL foils are made by Miller Engineering, and are sold in hobby stores to illuminate model railroad billboards. However, you could also pull out the LCD display EL (or LED) backlighting from an LCD clock or calculator. Figure 81 shows a few examples of spectral images obtained with our simple setup.
Figure 80 We coupled an inexpensive digital camera and a piece of EL foil to a Project STAR spectrometer to make it possible to capture light spectra for computer analysis.
Figure 81 Spectral images obtained with our simple spectrometer of Figure 80. Top scale is in electron-volts [eV]; lower scale is in nm.
We convert pictures taken with this spectrometer into spectral plots with VisualSpec, a free program created by Valérie Desnoux.† This program requires that spectral images be loaded in either .pic or .fit (the “Flexible Image Transport” standard that is commonly used by NASA to store and transfer astronomical images) format, so we convert the .jpg images produced by our camera using one of the free online image conversion tools. VisualSpec is very well documented, and includes excellent user instructions.
Now, turn on your hydrogen spectrum tube and observe the light through your spectroscope. Can you distinguish the Balmer lines? Well, in 1885, Balmer noticed that the lines get closer together, following a specific pattern as wavelength increases. Balmer figured out that lines appeared with regularity at certain multiples of 364.56 nm. He found the empirical formula:
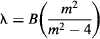
where λ. is the wavelength of a hydrogen line, B is Balmer’s constant with the value of 364.56 nm, and m is an integer greater than 2. Using this formula, Balmer was able predict lines in the invisible portion of the spectrum, which were later confirmed when instruments were invented to measure lines outside the visible spectrum.
In the 1880s, the Swedish physicist Johannes Rydberg was also working on the spectra emitted by the elements. He found out that he could simplify his calculations by using the wavenumber (the number of waves occupying a set unit of length, equal to 1/λ, the inverse of the wavelength) as his unit of measurement. When Balmer’s paper was published, Rydberg generalized the Balmer equation to include new hydrogen lines that were unknown when Balmer did his work (Figure 82). Rydberg’s formula is a simple reciprocal mathematical rearrangement of Balmer’s formula:
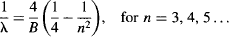
Figure 82 Spectral lines for the emission of hydrogen for n1 = 1, n1 = 2, and n1 = 3. Looking at them on a graph shows the pattern generalized by Rydberg in his formula.
Rydberg then generalized his formula to take into account a new series of lines being observed for the hydrogen atom:
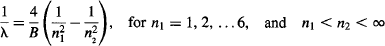
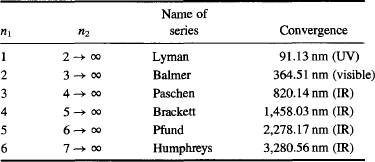
Today, 4/B is known as the Rydberg constant RH = 1.09737316 × 107 m−1 and is used in the formula to predict the complete spectrum produced by hydrogen. All of these series have been confirmed experimentally, as shown in Table 5.
TABLE 5 Spectral Lines Predicted by Rydberg for the Emission of Hydrogen and Later Confirmed Experimentally
Leave a Reply