In his third experiment, Thomson measured the mass-to-charge ratio (m/e) of the cathode rays. His setup allowed him to measure how much energy the rays carried and how much they were deflected by a magnetic field while also being deflected by an electric field.
Figure 50 shows a simplified version of the apparatus. A potential difference V accelerates electrons from the cathode toward the anode. Electrons then emerge out of the anode plate as a narrow beam. There are two large, parallel aluminum plates that are energized by a high-voltage supply to maintain uniform electric field E across a fluorescent screen overlaid with a reticule. A magnetic field is applied perpendicular to the plane of the screen. The electric and magnetic fields are directed at right angles to each other and also at right angles to the beam of electrons. For his experiment, Thomson adjusted the strengths of the two fields so that the upward deflection of the beam of electrons due to the electric field was completely cancelled by the downward deflection by the magnetic field. The charge of the electron e was unknown to Thomson at the time, so he estimated the electron’s velocity by measuring the deflection of the beam with only the magnetic field on, and once again with only the electric field on. Thomson reasoned:

Figure 50 For his third crucial experiment of 1897, Thomson measured the mass-to-charge ratio of the electron by using a magnetic field to balance the electrostatic deflection of a cathode-ray beam.
where the magnetic deflection in Thomson’s experiment is set to exactly balance the electrostatic deflection, so:
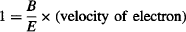
At the same time, the electron’s velocity may be found from the energy-balance equation for the kinetic energy acquired by the undeflected electron when accelerated by the accelerating voltage V:
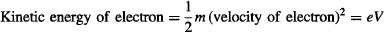
Replacing the velocity of the electron from the prior equations, and rearranging the terms to measure e/m:
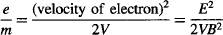
Thomson estimated m/e to be between 1.1 to 1.5 × 10−11 kg/Coulomb using his crude CRT. The modern value is 0.57 × 10−11 kg/Coulomb, so he did a very good job at estimating m/e’s order of magnitude, which allowed him to state that the mass-to-charge ratio of the new particle was over 1,000 times lower than that of the lightest atom known—a hydrogen ion (H+)—suggesting either that the particles were very light and/or very highly charged.
Thomson thus concluded:
As the cathode rays carry a charge of negative electricity, are deflected by an electrostatic force as if they were negatively electrified, and are acted on by a magnetic force in just the way in which this force would act on a negatively electrified body moving along the path of these rays, I can see no escape from the conclusion that they are charges of negative electricity carried by particles of matter.
In the years that followed, Thomson figured out ways of directly measuring e, allowing him to determine the mass of the negatively charged particles in cathode rays. The measurements showed that e is the same in magnitude as the charge carried by the hydrogen ion when water is split up by electrolysis. Thomson proved that the mass of the particles was less than 0.001 of the mass of the hydrogen atom—the smallest mass known at that time. Thomson believed the atomic diameter to be around 10−10 m, which is well within the modern range between 60 and 600 × 10−12 m. He also estimated the electron’s size to be approximately 10−13 m, which compares well to the so-called “classical electron radius” equal to 2.82 × 10−15 m.
Thomson called the particles that he discovered corpuscles.14 Today, we call these particles electrons after the “fundamental unit quantity of electricity” proposed by Irish physicist George Johnstone Stoney in 1891.
Leave a Reply