As we have seen, the standard model does a pretty good job with three of the four fundamental interactions of nature. Fitting gravity in remains a huge challenge. Another shortcoming related to this is that there are still a fairly large number of free parameters in the model. A free parameter refers to a quantity that is not predicted by the theory, but which the theory uses to calculate other quantities. If a theoretical model has a free parameter, the only way to know the value of that parameter is to measure it. The theoretical model gives us relationships between various parameters, so that once we manage to measure a few free parameters, the theory tells us what all the other parameters should be (e.g., the strength of a particular force or the probability of a certain event happening).
DEFINITION
The free parameters in a theoretical model are like necessary starting values. They are physical quantities which the theory needs to make its predictions, but the theory does not constrain or predict what the value of any free parameter actually is.
Physicists prefer theories that don’t have too many free parameters. After all, the more free parameters there are, the less the theory actually explains. The standard model has a relatively small number of elementary particles in it, but it still does not predict exactly what the mass of any of the particles should be (except for the massless cases, the photon and the gluons). It does predict that the antiparticles should have the same mass as the particles, but that leaves us with about 15 free parameters. The Higgs mechanism provides a theoretical explanation for why elementary particles may have mass, but it does not yet determine what those masses should be.
QUANTUM LEAP
Another deficiency of the standard model should be mentioned here, although we don’t yet know if this shortcoming has anything to do with quantum physics. There is convincing evidence from astronomy and cosmology that the hadrons and leptons we know about only make up about 15 percent of the total mass in the universe. The rest of the mass is influenced by gravity, but apparently not the strong or electromagnetic forces. We don’t have any idea what this stuff is yet, so we call it “Dark Matter.” This Dark Matter might turn out to be some new elementary particles we have yet to discover. With any luck, when we learn how to incorporate gravity into our quantum theory of everything, we’ll understand just what this Dark Matter is.
The standard model also fails to explain why there are three generations of elementary particles with different masses. The fact that there are three and only three generations is an observed fact, not a prediction of the standard model. The handful of fundamental constants (such as Planck’s constant, or the speed of light) also constitutes a set of free parameters, as are the relative strengths of the strong force and the electroweak interaction. A more satisfying theoretical model would tell us why these take the values that they do, or at least why they are arbitrary.
The standard model also fails to explain the presumed unification of the fundamental forces way back when the universe was much younger. Many physicists believe that the electroweak interaction and QCD can be unified under a common theoretical framework. These interactions, at least, are both described by quantum field theories. The electromagnetic, weak, and strong interactions now seem to have totally separate strengths and characteristics, but there is evidence that they could have once been manifestations of a common, more fundamental interaction.
The successful theoretical unification of electromagnetism and the weak interactions provides a model for unifying the strong interaction with these two. Our universe today is expanding and cooling, meaning that in the past it was hotter and denser. At some earlier time (billions of years ago, actually) the temperature and density were high enough that there was no difference between photons and the W and Z bosons which today mediate the weak interaction. Thus the electromagnetic and weak interactions were essentially the same force.
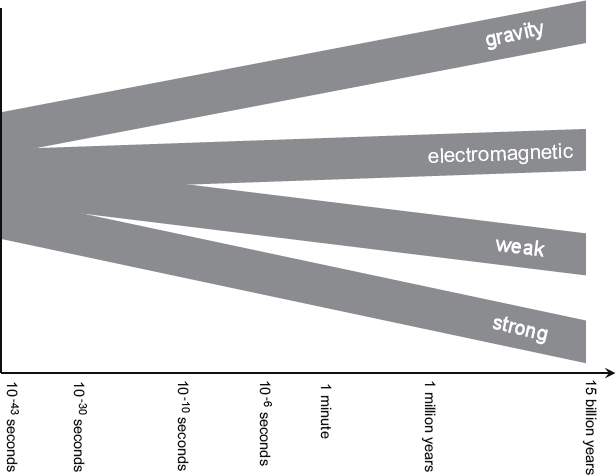
This schematic illustrates the potential unification of the fundamental interactions at much earlier times. The numbers along the horizontal axis indicate the approximate age of the universe.
As the universe cooled, the symmetry between electromagnetism and the weak interaction was broken. Physicists often draw an analogy with a phase change, such as the freezing of a liquid. In the liquid state, matter looks the same in every direction. But when the liquid freezes, it may become crystallized, which means there are now differences in the structure of the material in different directions. The latter state is thus less symmetric than the former.
While today the strong interaction seems very different from the electroweak, the fact that quarks (strong interaction) have just the right electric charge to balance that of electrons (electromagnetic interaction), suggests that there must be some underlying symmetry between these two sectors. The fact that the incredibly strong coupling between quarks gets weaker with increasing energy also gives us hope for a similar scenario. If we go to even earlier times in the history of the universe (less than 10-30 seconds after the beginning), the energy density would have been high enough that gluons would have behaved the same way as photons, and a single quantum field theory could have described perfectly all of the interactions between quarks and leptons.
A quantum field theory which unifies the strong, weak, and electromagnetic interactions is called a grand unified theory, or GUT. Physics doesn’t actually have a well-developed GUT yet, but the term is used to distinguish this level of unification from the ultimate goal. The term theory of everything (or ToE) has actually come into common use in the physics world. As distinct from a GUT, a theory of everything would unite all of the fundamental forces, including gravity.

DEFINITION
A grand unified theory (or GUT) is a common quantum field theory that unites the electromagnetic, strong, and weak interactions.
A theory of everything (or ToE) is a unification of the electromagnetic, strong, and weak interactions with gravity.
The Theories of Relativity
Before we look at recent attempts to incorporate gravity into quantum physics, we need to take a closer look at the best current theoretical model for gravity itself.
Einstein’s “theory of relativity” can be divided into two parts. The first part is referred to as special relativity, because it treats a fairly narrow special case of relative motion. Special relativity shows us how to deal with objects that are traveling at a constant velocity relative to each other. General relativity is able to include changes in velocity, which we call acceleration. It turns out that by including acceleration, general relativity can account for the force of gravity at a very fundamental level.
QUANTUM LEAP
Both parts of Einstein’s relativity theory were actually published and well-known before modern quantum physics came to be. Special relativity came out in 1905, and general relativity in 1915.
Why is gravity so different from the other forces? The key to understanding this is to visualize mass in two different ways. Think about the classical electrostatic force. Only particles with non-zero electric charge can attract or repel each other due to the electromagnetic interaction. When such a force exists, it causes the charged particle to accelerate, according to Newton’s second law: F = ma, or equivalently, a = F⁄m. The “source” of the force (F) is the electric charge, and the effect of the force (acceleration, a) is inversely proportional to the mass (m). The same force has less effect on a greater mass. The electric charge and the mass play two completely different roles.
In the case of gravity, however, mass plays both roles. It is now the “source” of the force, in that only particles with mass will feel the force of gravity, and the force felt is directly proportional to the mass. On the other side, the effect of the force is still hindered by mass through F = ma. Physicists differentiate the two types of mass as “inertial mass” (the one that determines how difficult it is to accelerate an object) and “gravitational mass” (the one that determines how strong the gravitational force will be, like the charge).
Experiments have shown that in all cases, inertial mass is exactly the same as gravitational mass. Faced with such an amazing coincidence, physicists naturally search for a reason that this should be the case. Einstein made a bold postulate, called the equivalence principle, to explain this. Realizing that the force we call gravity was indistinguishable from the effect of acceleration, he suggested that these two things were actually equivalent.

DEFINITION
The basis for Einstein’s theory of general relativity, the equivalence principle, states that the effect of gravity is indistinguishable from the effect of a uniform acceleration, so that the two situations are exactly the same.
General relativity uses the equivalence principle to explain gravity in purely geometric terms. To do so, it must deal with the very structure of what we know as space and time. These aspects of nature always existed passively in the background of classical physics—some sort of absolute, unchanging scaffold, relative to which all of our measurements were made. General relativity unites space and time into one thing, called spacetime, and that thing now plays a much more active role in natural phenomena. No longer unchanging, spacetime is distorted by the very presence of mass and energy in the universe. The distortions move and change as mass and energy move around.
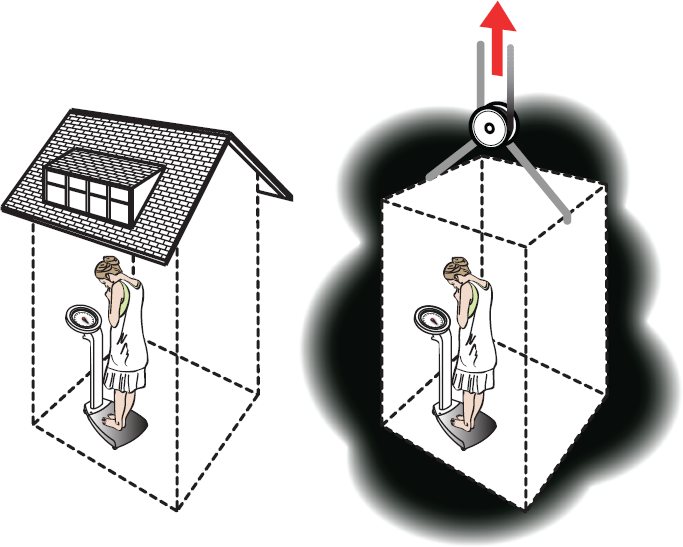
“Einstein’s elevator” is a useful device used to describe the equivalence principle.
This is illustrated by the example known as “Einstein’s elevator.” At left, we peek into a closed, windowless shed sitting on the surface of the earth. Inside, a woman is weighing herself on an ordinary scale. The scale indicates her correct weight by measuring the force of her feet pressing down on it. We interpret that force as being due to gravity attracting the woman to the earth below.
At right, we look inside a closed elevator car out in deep space, far from any other masses. Inside, the same woman is standing on the same type of scale. If the whole car is accelerating “upward” at just the right rate, the scale will read the same as it did in the closed shed. This time, instead of measuring the force of gravity, it will be measuring the force that the scale exerts on the woman’s feet in order to make her accelerate up with the car. With no windows to look out of, every observable thing in the closed elevator car appears exactly the same as in the closed shed.
General relativity and its spacetime concept bears little resemblance to a quantum field theory. Gravity is not even treated as a force in general relativity. Instead, particles with mass naturally follow paths that would seem to be straight lines relative to the curvature of the space itself. If it appears to us as though two masses are attracted to each other, it is really just a consequence of one mass distorting the space in which the other mass moves.
Not only that, but general relativity predicts that even massless photons are affected by gravity, due to that same distortion of spacetime. In the standard model, particles with zero mass (like the photon) can’t feel the gravitational force. This is another indication that our best theory of gravity is incompatible with the standard model of particle physics.
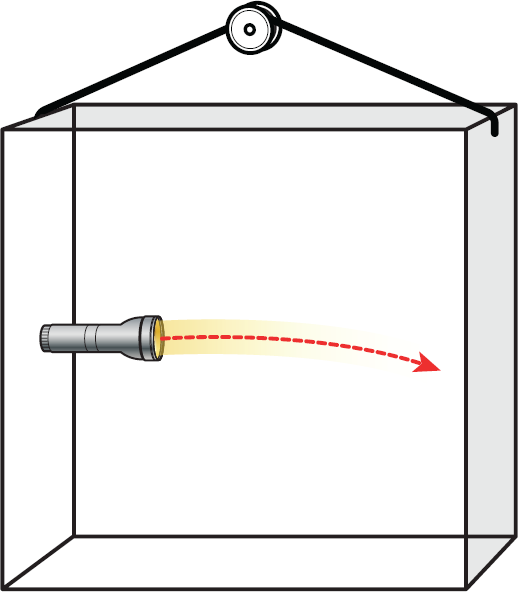
The “Einstein’s elevator” analogy can be extended to illustrate the effect of gravity on massless photons.
One way to visualize the idea that massless photons can be affected by gravity is to picture another windowless elevator car (or shed) as in the last figure. This time, a flashlight shines a beam of light across the room horizontally. If the car is actually accelerating upward, then the beam of light will appear to curve slightly downward as it travels from left to right. If the equivalence principle is true, that means that light will also curve if the car is stationary in a gravitational field. So general relativity predicts that photons are influenced by gravity, unlike the standard model, in which photons are massless. This prediction of general relativity has now been verified by many observations of light bending in the presence of strong gravitational fields.
General relativity has had great success in accounting for all known phenomena associated with gravitation. It correctly predicts that the path of light gets bent in the presence of mass concentrations, the existence of black holes, the large-scale structure of the universe, rapidly accelerating elevators, etc. All of these successes make it very difficult to throw out general relativity in order to replace it with a quantum field theory for gravity. Instead, theorists have sought ways to adapt general relativity into a quantum framework. But with such a radically different model of the force, it has been a tough nut to crack.
Leave a Reply