After the quantum revolution of the 1920s and 1930s, theoretical physicists developed a powerful way to deal with interactions that is consistent with all the requirements of quantum physics we have outlined so far. This approach essentially “quantizes” the force fields that were inherited from classical physics. It makes explicit use of the basic symmetries in nature, which are closely connected to the conservation laws, and from the start it was made consistent with Einstein’s special theory of relativity. The general term for this approach is quantum field theory. The details of the math are beyond this book, but we will try to give a sense for how it works.
The best way to visualize the workings of a quantum field theory is to imagine all interactions between particles as being mediated by other particles. We can easily picture this if we have a basic appreciation for the conservation of momentum. Rockets are able to blast off and guns recoil when fired because of this conservation law.
Imagine standing still on a very slick surface, say the smoothest ice rink in the world, wearing your most slippery-soled shoes. And, you just happen to be carrying a pair of heavy fruitcakes. If you decide to hurl a fruitcake horizontally to the north, you will immediately start to slide to the south. While sliding south in a straight line, if you fling the second fruitcake to the east, your path will be diverted slightly to the west.
Now say you have a friend on the side of the rink with her own batch of fruitcakes. If you were standing still on the ice and she threw one at you, you would start moving the instant you caught it, in whatever direction the fruitcake was flying. Catching a flying fruitcake while in motion would also alter your path, all for the sake of conserving momentum.
We realize this sounds absurd, but stay with us. Suppose you and your friend both have on your slippery shoes, and are gliding along on the ice rink in almost, but not exactly, the same direction. You are separated by a few meters, but your paths are slowly getting closer together. Shortly before you collide, you hurl a fruitcake as hard as you can in her direction. This causes your path to turn slightly away from hers. If she catches the cake you threw, her path will also be slightly altered, in a direction away from yours.
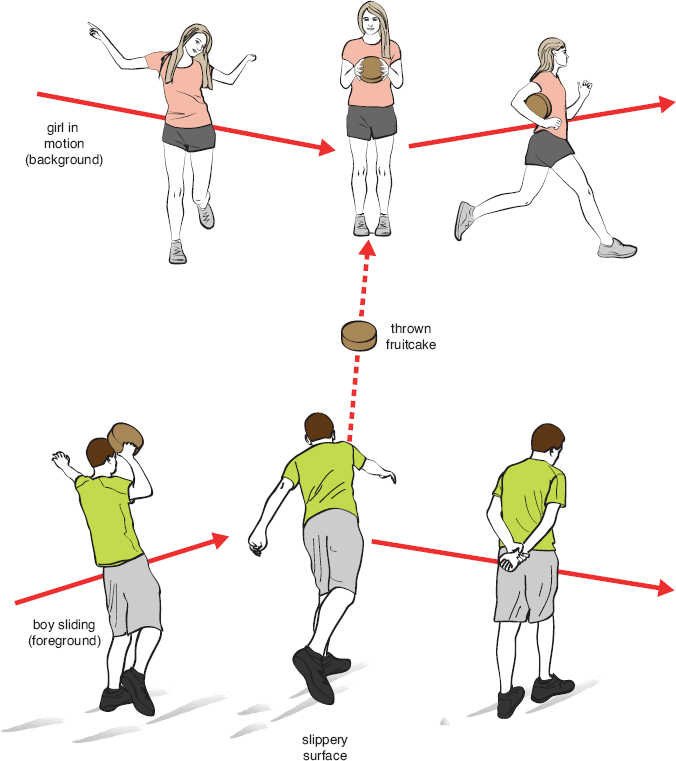
A repulsive force between two people on a frictionless surface can be modeled by the exchange of a massive object between them. The change in motion is simply a consequence of the conservation of linear momentum.
The result of all this is that, if someone were observing the two of you from some distance above, and if they could not see the fruitcake, it would appear as though an invisible, repulsive force pushed the two of you apart just as you were getting closer together. If you exchanged a whole bunch of fruitcakes in this manner, it would even look like the force was causing your paths to curve nice and smoothly.
This particle exchange model is the basis for all interactions in quantum field theory. It is the underlying basis for the field theories specific to the electromagnetic, the strong, and weak interactions. A common theme among them all is that all the fruitcakes are one type of particle and all the fruitcake hurlers are another. The matter particles, which exchange force-carrying particles, are always fermions. The force-carrying particles themselves are always bosons.
This exchange model does lots of nice things for us. It gets rid of the conceptual problem of forces magically acting at a distance without any contact—something that has bothered lots of physicists since Newton. It naturally takes into account the speed of light as the universal speed limit: no exchanged particle can travel faster than the speed of light, so no force can change its effects any faster than this. Perhaps most important, it quantizes the classical concept of a field in the form of discrete, exchanged (virtual) particles. To get a better grasp of how this all works, let’s now consider the three specific quantum field theories.
Leave a Reply