Superposition and Collapse

We explain that there is typically more than one solution to the Schroedinger equation for a given quantum system. Each solution is an Eigenfunction that we can denote as Ψ_i, and the various Eigenfunctions correspond to valid quantum states of the system. We also explained that any linear combination of Eigenfunctions is itself a valid solution and therefore a valid quantum state. For example, if Ψ₁, Ψ₂, Ψ₃ are valid quantum states then so is, say, Ψ = 3Ψ₁ + 1Ψ₂ + 5Ψ₃. Such a combination is called a superposition state, drawing on the concept of wave superposition that we introduce.

What we haven’t mentioned yet is that if we were to decide to take a peek and see which quantum state our system is in, we would not find it in any sort of superposition state. Instead, the laws of quantum physics tell us that we will find only a pure state (e.g., Ψ₁ or Ψ₂ or Ψ₃). The act of observing the system (or making any sort of “measurement”) instantaneously reduces the system to one and only one of its valid quantum states. Physicists refer to this as the collapse of the wave function.

DEFINITION

A superposition state for any given quantum system is an arithmetic (linear) combination of valid quantum states; it is itself a valid quantum state for the system.

Wave function collapse is the instantaneous transition from all possible valid quantum states to a single quantum state during the process of measurement or observation.

Moreover, the numbers that precede the Eigenfunctions (the “coefficients”) on the right side of the superposition we wrote down above are tied to the probability that you will find the system in the corresponding Eigenfunction when you take a look. More precisely, the square of each coefficient gives the relative probability of observing the corresponding Eigenfunctions. In the preceding example, you are 3² = 9 times more likely to observe Ψ₁ than Ψ₂, and 5² = 25 times more likely to observe Ψ₃ than Ψ₂.

This collapse of a wave function is mysterious in a number of ways. First of all, so far as we can tell, it happens instantaneously. In classical physics, when a variable describes a real physical quantity, its value changes smoothly in time, taking all the intermediate values between its starting and ending points. Even if the change is quick, it takes a certain amount of time to undergo the change (not zero). An instantaneous change, one that takes no time whatsoever, is difficult to handle mathematically. In classical physics, such an event would be ruled out as physically impossible.

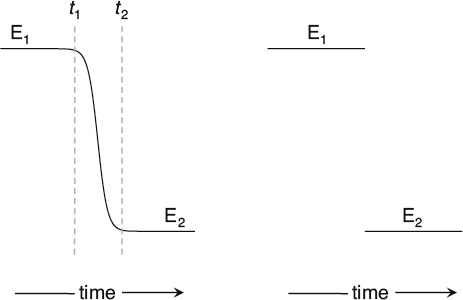
A continuous (left) vs. an instantaneous (right) transition.

On the other hand, quantum physics has introduced this kind of discontinuity elsewhere, so maybe we just have to get used to it. When electrons in atoms change their energy levels during a quantum jump, they don’t pass through the energies in between, and photons appear or disappear instantaneously. The collapse of the wave function could be like this, and at least there would be some internal consistency within quantum physics. In any case, the Copenhagen interpretation doesn’t say anything more about what happens to a wave function during the act of measurement (collapse).