When performing their experiment with various kinds of atoms, they did indeed see separate bands corresponding to discrete deflections, indicating that angular momentum was quantized in direction and magnitude. However, when they tried it with silver atoms, which should have l = 0 (no orbital angular momentum for the outermost electron), they observed two distinct deflections, equally above and below the spot corresponding to zero magnetic field. Since two is not an odd number, this was really quite something to see.
In 1927, T. E. Phipps and J. B. Taylor conducted an analogous measurement with hydrogen atoms. Since hydrogen atoms are so simple, this should have eliminated any uncontrollable effects in those complicated silver atoms. Yet, once again, half of the atoms were deflected up, and the other half down. The amount of the deflection was the same up and down. All this implied that electrons have some other type of angular momentum besides that caused by their orbital motion. This new angular momentum seemed to be an intrinsic property of the electrons themselves.
The amount of this angular momentum was particularly interesting. If the experiment is really measuring only two quantized directions for this vector, then we can’t be talking about a whole number value for its magnitude. In 1925, Samuel Goudsmit and George Uhlenbeck pointed out that everything would work out just fine if this new angular momentum, which we will call s, had a magnitude of s = 1⁄2.
If this were the case, the range of possible projections onto any preferred axis would extend from –s to +s. This would mean, therefore, two possible values: –1⁄2 or +1⁄2. This new degree of freedom eventually took on the name “spin,” since it was as if the electron was spinning like a top. A spinning top also has two possibilities: clockwise or counter-clockwise rotation.
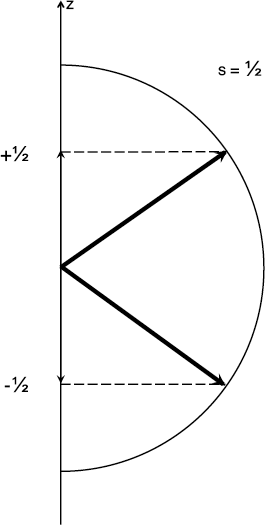
The spin angular momentum vector has a quantum number s = 1⁄2, along with the corresponding projections of –1⁄2 and +1⁄2.
Spin angular momentum is quantized in magnitude and direction just like orbital angular momentum. There are some important differences, however. The spin is a property of the electron regardless of whatever potential energy it finds itself in. And every electron has the same amount of spin. If the angular momentum quantum number associated with this spin is 1⁄2, as postulated by Goudsmit and Uhlenbeck, then the two possible projections, 1⁄2 and –1⁄2, are separated by one unit, just like for orbital angular momentum. These two equal but opposite directions for the spin would explain the Stern-Gerlach results, as well as some fine structure that was being observed in spectral lines of other atoms. Since there are only two possible directions (or states) for a spin 1⁄2 particle, we usually call these states “up” and “down”.
ATOM TRAP
Though physicists use the word spin to talk about an electron’s intrinsic angular momentum, it is really a misnomer. It can’t possibly be true that the electron is actually spinning to account for this extra angular momentum. Given its small size, an electron would have to spin much faster than the speed of light, which we know to be the universal speed limit for all moving matter.
The explanation for the origin of particle spin had to wait for the Schroedinger equation to be cast in a form consistent with the theory of special relativity. It had been about 20 years since Einstein had published his first papers on this subject, so its revolutionary ideas were well known to the physics community and largely accepted. The Schroedinger equation we presented was strictly a nonrelativistic version, treating space, time, and energy in the old classical ways. This was expected to be a good approximation for systems with relatively low energies (true of quantum physics) and speeds much less than the speed of light.
However, considering Heisenberg’s uncertainty principle and the small volumes occupied by electrons in atoms, some portion of electron wave functions could have speeds approaching (though not exceeding) the speed of light. It was widely held at the time that a relativistic version of Schroedinger’s equation would eventually be needed. The problem was that it was a very tall order to actually derive this. Schroedinger himself tried, but came up with something that conflicted with experiment so he eventually gave up on it.
In 1928, the British physicist Paul Dirac finally figured out how to transform Schroedinger’s equation into the proper relativistic form. One consequence was that the mathematics required to solve the equation became a lot more complicated. But another very important consequence was that once you finally work through all that, the concept of spin 1⁄2 particles came naturally out of that math.
QUANTUM LEAP
Special relativity cast the universe not in three dimensions but four—the three usual directions of space plus that of time. It is therefore only natural that this theory, and its additional degree of freedom, should result in a fourth quantum number.
Dirac was specifically trying to explain the behavior of particles with spin quantum number equal to 1⁄2, like the electron. But lots of other particles turn out to have spin as well. Again, this quantum mechanical spin is an intrinsic property of the particle, like its mass or electric charge. The spin of a particle can’t be changed, and all particles of the same type have the same amount of spin. Besides electrons, protons and neutrons also have spin = 1⁄2. Even our old friend the photon has spin, but in its case the whole-number value of 1. Other particles are known which have spin 3⁄2, others have spin = 2, and still others have a spin quantum number of zero.
Leave a Reply