When we presented our examples in one dimension, the Schroedinger equation gave us bound states with quantized energy. In case you didn’t notice, only one quantity ended up being quantized: energy.
Why do we care? Well, it turns out that when you solve the Schroedinger equation in higher dimensions, you end up with more than one quantization condition. In fact, the actual number of dimensions determines precisely how many physical quantities will be quantized! More accurately, there will be as many quantized quantities as there are “degrees of freedom” in the physical situation. A degree of freedom is just what it sounds like: in how many ways or independent directions is the particle free to move in? That’s how many degrees of freedom it has.
You encounter three degrees of freedom each and every day. If you stand up from your armchair (one), you can walk forward to the kitchen for another cup of coffee (two), or you can walk to the right to let out the dog (three). Conversely, the simplistic problems we dealt with earlier only had one degree of freedom (which we called “x”).
When walking about your house, it is best to think of the three degrees of freedom as three directions at right angles to each other (like length, width, and height). For a spherical system like a hydrogen atom, however, it is a lot more natural to use what we call a “spherical” coordinate system. Without going into the details, the three natural degrees of freedom are the distance from the central nucleus along with two angles to describe the position at that distance (rather like latitude and longitude on the earth).
Three-dimensional space can be represented using standard rectangular coordinates (left) or using something known as spherical coordinates (right). In both cases, three independent variables are needed to cover the three degrees of freedom.
When you do the math, the three things that must be quantized for electrons in the hydrogen atom are energy, the magnitude of the angular momentum, and the direction of the angular momentum vector (as characterized by its projection onto any given direction). That might sound more complicated than it really is. An important aspect of angular momentum is that it is a vector quantity.
DEFINITION
A vector is a quantity that has both a magnitude and a direction in space. It is rather like an arrow of a certain length pointing in a certain direction.
Vectors are the sort of physical quantities for which direction is just as important as the magnitude. The same amount of angular momentum can be oriented in different directions. If we select a preferred direction in space (calling it, say, z), then every different orientation of the vector would “project” a different amount of the angular momentum along that preferred direction (like an object casting a shadow). If there was ever a case where a figure would help, this is probably it.
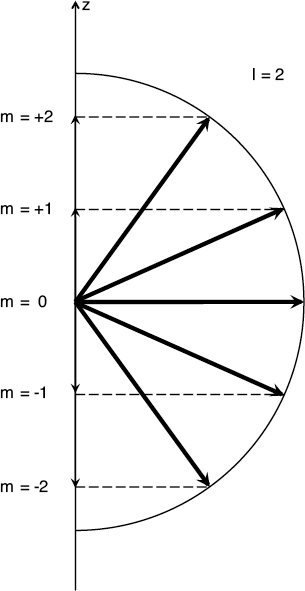
When an angular momentum vector changes direction relative to some fixed axis (which we call z here), its projection along that axis changes, too. Here we depict the angular momentum vector for quantum number l = 2, along with the corresponding projections m = -2, -1, 0, 1, and 2.
To recap: when solving the Schroedinger equation for the hydrogen atom, we discover that not only is the magnitude of the electron’s angular momentum quantized, but so is its projection along the vertical axis of our spherical coordinate system. That is a new feature that only comes into quantum mechanics in three dimensions.
Since all of these quantized things take only certain discrete values, we can label them with whole numbers. The so-called “principal” quantum number is related to the energy of the state, and we use the letter “n” to label it. This is the same principal quantum number we encountered and the same one that figures into the atomic energy levels. The lowest energy state is labeled n = 1, and integers greater than 1 correspond to states of higher energy.
The lower case letter l is used to label states with certain values of the angular momentum magnitude. This quantum number can only take whole-number values between zero and n-1. That means that for the lowest energy state of the electron (n = 1, which we call the “ground” state) the only possible value for the angular momentum is zero. This is another difference between older models of the hydrogen atom, which assumed all orbits must have some angular momentum, and the modern one, where zero angular momentum is permitted.
The letter m is conventionally used to label the orientation of the angular momentum (in terms of its projection along some preferred axis). This can only take whole-number values between –l and l. The actual amount of angular momentum is found by multiplying certain combinations of these quantum numbers by Planck’s constant. This all sounds a lot more complicated than it really is, so let’s write it down in the form of a table.
Leave a Reply