The simplest case we can look at is that of a free particle—that is, a particle traveling through space under no influence of external forces. A real-world example would be the electrons that emerged from J. J. Thomson’s cathode ray tube before they were acted upon by his electromagnetic fields. To find the wave function in this case, we must simply use the Schroedinger equation when the potential energy function U is exactly zero everywhere (in one dimension). Let’s label our one dimension x.
DEFINITION
A particle moving through a region of space where no external forces act upon it is considered to be a free particle.
The wave function for a free particle is called a plane wave, which is formed by two sine functions, one real and one imaginary.
The only interesting solutions to the Schroedinger equation for zero potential energy are functions called plane waves. Although these wave functions are complex, both the real parts and the imaginary parts are just sine functions traveling along the x-direction with constant amplitude, simple waves we have seen before.
The allowed solutions include waves traveling in the positive or the negative x-direction. It also includes waves traveling in both directions in the same wave function at the same time. Mathematically this is perfectly permissible, and the combination can have any proportion of forward- and backward-moving wave components.
For simplicity, let’s consider plane waves moving in only one direction. Any such wave function has a definite momentum along the x-direction and constant amplitude. Definite momentum means that there is no intrinsic uncertainty, while constant amplitude means that the probability of finding the particle is the same at all values of x.
This last statement should sound pretty strange if you think about it. In our simple picture, x has no boundaries. It can extend 50 zillion miles (and farther) in either direction. The fact that the probability of finding the particle at any x over an infinite range means you can actually have absolutely no idea where the particle is! If it is equally likely to be found literally anywhere, then it doesn’t really have any position at all.
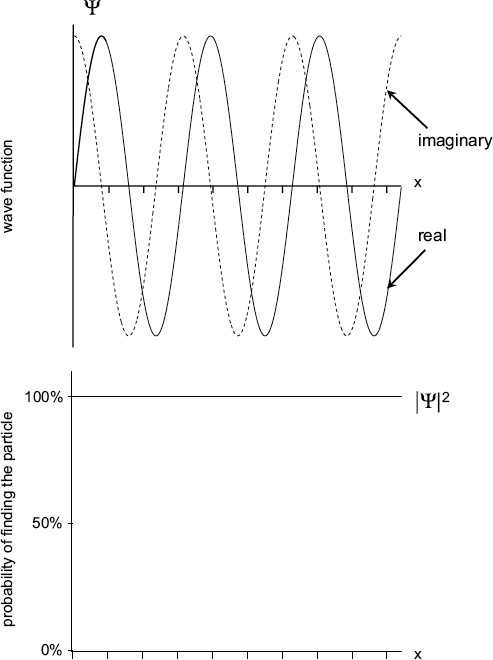
The wave function for a free particle is formed by two sine functions—one real and one imaginary (top). Since its momentum is known with certainty, it can be found anywhere in the universe with 100 percent probability (bottom).
This is just another case of quantum weirdness stemming from Heisenberg’s uncertainty principle. As you recall, momentum and position form a conjugate pair, and the product of their uncertainties has a certain minimum value. The limiting case of this is where one of the quantities in the pair (momentum, for example) is definitely known. In such a case, the other is completely unknown, which is just another way of saying the uncertainty (for the position in this case) is infinitely huge.
Although this example has the virtue of simplicity, it is not very realistic for a single particle. The plane wave solution can, however, serve as a pretty good description of a continuous beam of particles, provided the particles making up the beam all have about the same momentum, don’t interact with each other very much, and come through at a constant rate.
Also, in cases where the momentum is not known with perfect certainty, we end up with plane waves of slightly different wavelengths. These can be added together to make more localized wave packets, as we saw earlier. All the different component waves that make up a localized wave packet are valid solutions of the Schroedinger equation with no potential energy.
There is one more important aspect of plane waves we should mention. With constant or zero potential energy, the Schroedinger equation places no restriction on the energies of any of the solutions. The plane waves we have been talking about can have any positive value for their energy. In this case, energy is not quantized.
Leave a Reply