We made a big deal about the use of mathematical models to describe physical phenomenon. Now we’ll take a crack at seeing not only how this can be done, but why it turns out to be so useful. And, given the emphasis we’ve been placing on matter waves, it’s probably no surprise that our starting point will be a mathematical model to describe the wavy behavior of matter waves.
Fortunately for us, mathematicians have studied waves for millennia. The sine function has been used for at least 1,500 years, and has been mastered by high school students for nearly as long. In mathematical form it is given by y(x) = sin(kx+ωt), where k is inversely proportional to the wavelength (λ) and ω is directly proportional to the frequency (f). The meaning of “y(x)” is simply that for every possible value of x, there is one corresponding value for y that can be calculated using the mathematical equation.
This fact can be used to turn the mathematical equation into a two-dimensional graph by selecting values of x, computing y, and then putting a point on a two-dimensional graph at the right location relative to the x and y axes. When you do this for all values of x, you end up with a nice wavy line as shown in the corresponding figure. Since this looks like a decent way to model a wave mathematically, we will select the sine function to represent a matter wave moving in space and time.
If we set the wavelength of our expression equal to the value given by Louis de Broglie’s relation for a particle having a certain momentum, then we will have constructed an expression that represents the matter wave associated with that particle. We could even be so bold as to call this expression a wave function for the particle, since it would yield a unique value for every location in three-dimensional space. Of course, these values would vary with time, but that’s no big deal since the wave function would also tell you exactly how they vary. The function would have all the characteristics we associate with waves: frequency, wavelength, speed, and amplitude.
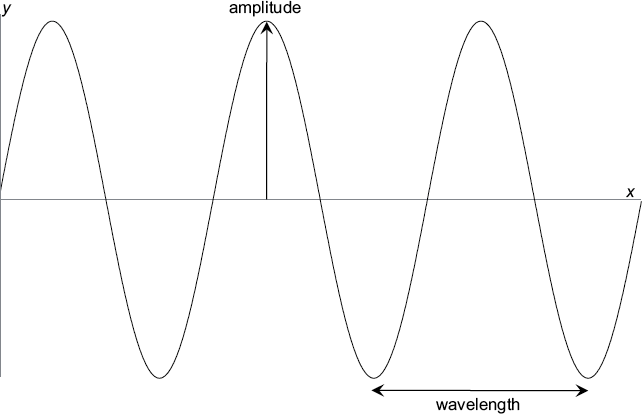
This is a plot of a wave function for a matter wave frozen at one instant of time. For every value of x there is a corresponding value of y that can be calculated using our sine function. In this case, we happen to know the exact momentum (mass and velocity) of the particle. We assume that the wave is traveling to the right, so that a short time later, the whole pattern would be shifted to the right by an amount that depends on its speed.
While our wave function is oscillating, it rises equally above and below zero. For what is to come, it is crucial to understand what we mean by amplitude: the amplitude of a wave is simply the size of the oscillation above or below zero. A wave rising one unit above zero has an amplitude of one, while a wave dropping one unit below zero also has an amplitude of one.
DEFINITION
Matter waves are waves associated with massive particles in motion. The actual value of a matter wave is not observable, but the amplitude squared of the wave gives the probability of observing the particle at a particular location.
The wave function is the mathematical description of a matter wave. It gives the value of the wave at all points in space and time relevant to a certain particle in a certain state.
If we want this wavy thing to have some relation to the real world, we have to explain what the value of the wave function means physically. In order to do this, let’s exploit the symmetry between light and matter that inspired de Broglie in the first place. Photons are chunks of energy associated with electromagnetic waves. But the photons themselves are not the waves. Photons do not oscillate in position or time; rather the oscillations come from the corresponding electromagnetic field. That electromagnetic field, in turn, can be measured directly by its effect on charged particles.
Einstein’s theory of relativity showed us that mass is a form of energy. So in analogy with light, massive particles (like electrons) can be considered to be chunks of energy associated with matter waves. Again, the particles themselves are not waves. They don’t oscillate up and down as they travel. However, in the case of matter, the associated waves cannot be measured directly through interactions with other physical entities. Instead, we have to resort to indirect ways of measuring matter waves. Fortunately, we have other measures at our disposal.
ATOM TRAP
Since we think of light as both waves and particles, it is a common misconception to imagine the particles (photons) themselves traveling along a wavy path. We must try to keep the complementarity of the two pictures in mind. If viewed as a particle, the photons travel in straight paths (until they bounce off of something or get absorbed). The associated waves are periodic changes in the strengths of the electromagnetic field, so there is no actual motion of the photon perpendicular to the direction in which the wave (or photon) travels. The same idea applies to matter waves associated with massive particles.
Think back to the two-slit interference experiment with light. Thomas Young observed a pattern of light and dark stripes on the screen located some distance past the two slits. From the wave point of view, the brightest parts of the pattern correspond to locations of constructive interference, where the amplitude of the resulting wave was greatest. From the particle point of view, the bright lines correspond to areas where photons are most likely to land during any period of time. If a device is set up to detect individual photons, the developing interference pattern would build up over time exactly like the last figure.
Leave a Reply