Bugs in the boundaries of the input domain are common in software systems. As developers, we have all made mistakes such as using a “greater than” operator (>) where it should have been a “greater than or equal to” operator (>=). Programs with such bugs tend to work well for most provided inputs, but they fail when the input is near the boundary. Boundaries are everywhere, and our goal in this section is to learn how to identify them.
When we devise partitions, they have close boundaries with the other partitions. Imagine a simple program that prints “hiphip” if the given input is a number smaller than 10 or “hooray” if the given input is greater than or equal to 10. A tester can divide the input domain into two partitions: (1) the set of inputs that make the program print “hiphip” and (2) the set of inputs that make the program print “hooray”. Figure 2.2 illustrates this program’s inputs and partitions. Note that the input value 9 belongs to the “hiphip” partition, while the input value 10 belongs to the “hooray” partition.
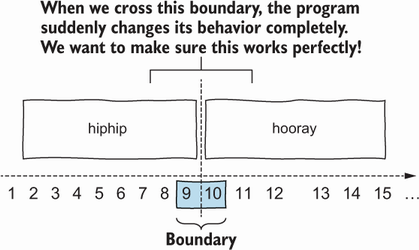
Figure 2.2 The boundary between the “hiphip” and “hooray” partitions. Numbers up to 9 belong to the “hiphip” partition, and numbers greater than 9 belong to the “hooray” partition.
The odds of a programmer writing a bug near the boundary (in this case, near the input values 9 and 10) are greater than for other input values. This is what boundary testing is about: making the program behave correctly when inputs are near a boundary. And this is what this fourth step is about: boundary testing.
Whenever a boundary is identified, I suggest that you test what happens to the program when inputs go from one boundary to the other. In the previous example, this would mean having a test with 9 as input and another test with 10 as input. This idea is similar to what Jeng and Weyuker proposed in their 1994 paper: testing two points whenever there is a boundary. One test is for the on point, which is the point that is on the boundary; and the other test is for the off point, which is the point closest to the boundary that belongs to the partition the on point does not belong to (that is, the other partition).
In the hiphip-hooray example, the on point is 10. Note that 10 is the number that appears in the specification of the program (input >= 10) and is likely to also be the number the developer uses in the if statement. The value 10 makes the program print “hooray”. The off point is the point closest to the boundary that belongs to the other partition. In this case, the off point is 9. The number 9 is the closest number to 10, and it belongs to the “hiphip” partition.
Let’s discuss two more common terms: in point and out point. In points are points that make the condition true. You may have an infinite number of them. In the hiphip-hooray example, 11, 12, 25, and 42 are all examples of in points. Out points, on the other hand, are points that make the condition false. 8, 7, 2, and –42 are all examples of out points. In equalities, the in point is the one in the condition, and all others are out points. For example, in a == 10, 10 is the (only) in point and the on point; 12 is an out point and an off point; and 56 is an out point. Whenever you find a boundary, two tests (for the on and off points) are usually enough, although, as I will discuss later, I do not mind throwing in some interesting in and out points to have a more complete test suite.
Another common situation in boundary testing is finding boundaries that deal with equalities. In the previous example, suppose that instead of input >= 10, the specification says that the program prints “hooray” whenever the input is 10 or “hiphip” otherwise. Given that this is an equality, we now have one on point (10) but two off points (9 and 11), because the boundary applies to both sides. In this case, as a tester, you would write three test cases.
My trick to explore boundaries is to look at all the partitions and think of inputs between them. Whenever you find one that is worth testing, you test it.
In our example, a straightforward boundary happens when the string passes from empty to non-empty, as you know that the program stops returning empty and will (possibly) start to return something. You already covered this boundary, as you have partitions for both cases. As you examine each partition and how it makes boundaries with others, you analyze the partitions in the (str, open, close) category. The program can have no substrings, one substring, or multiple substrings. And the open and close tags may not be in the string; or, more importantly, they may be in the string, but with no substring between them. This is a boundary you should exercise! See figure 2.3.
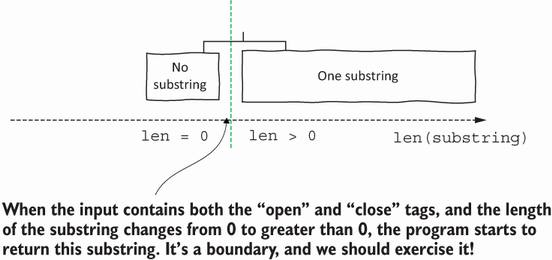
Figure 2.3 Some of the boundaries in the substringsBetween() problem.
Whenever we identify a boundary, we devise two tests for it, one for each side of the boundary. For the “no substring”/“one substring” boundary, the two tests are as follows:
strcontains bothopenandclosetags, with no characters between them.strcontains bothopenandclosetags, with characters between them.
The second test is not necessary in this case, as other tests already exercise this situation. Therefore, we can discard it.
Leave a Reply