CONE CLUTCH

In cone clutch, the friction surfaces make a cone of an angle 2β (Figure 16.6). The normal force on the cone is  where β is semi-cone angle. The main advantage of cone clutch is that the normal force is increased, since sin β ≤ 1.

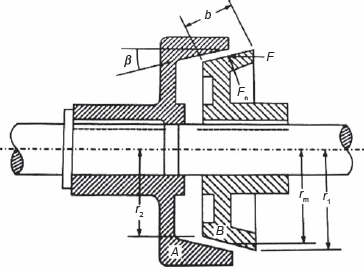
Figure 16.6 Cone Clutch

Torque for Uniform Pressure

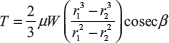
Torque for Uniform Wear

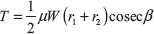
Example 16.4: A cone clutch having a mean diameter of 200 mm and semi-cone angle of 12.5° transmits a torque of 200 N m. The maximum normal pressure at the mean radius is 0.1 N/mm². The coefficient of friction is 0.25. Calculate the width of the contact surface. Also, find the axial force to engage the clutch.

Solution:

Given: R_m = 200 mm, β = 12.5°, T = 200 Nm, P = 0.1 N/mm², μ = 0.25

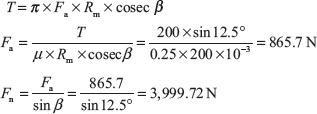
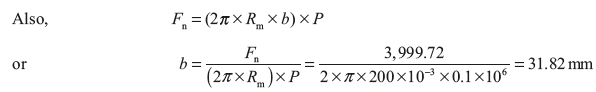
Example 16.5: A cone clutch has cone angle of 25°. Maximum pressure between contact surfaces is limited to 0.25 N/mm² and width of contact surface is half of the mean radius. Find the radii of the conical surface to transmit 20 kW at 1,500 rpm assuming uniform wear condition. Coefficient of friction is 0.25.

Solution:

Given: β = 12.5°, P = 0.25 N/mm²,  Power = 20 kW, N = 1500 rpm, μ = 0.25

Solving Eqs (16.1) and (16.2), we get

 

r₁ = 91.28 mm

r₂ = 81.92 mm