In a single plate clutch, a flywheel ‘A’ is bolted to a flange on the driving shaft B. The friction plate C is fixed to a hub which can slide on the spline, i.e., driven shaft ‘D’. Two rings of friction material are riveted to flange ‘A’ and the plate ‘C’. The pressure plate ‘E’ is bushed internally, so as to revolve freely on shaft D and is integrated with withdrawal force F. A number of spiral springs are arranged around the clutch at ‘S’ as shown in Figure 16.4 (a), which provides axial thrust between friction surfaces.
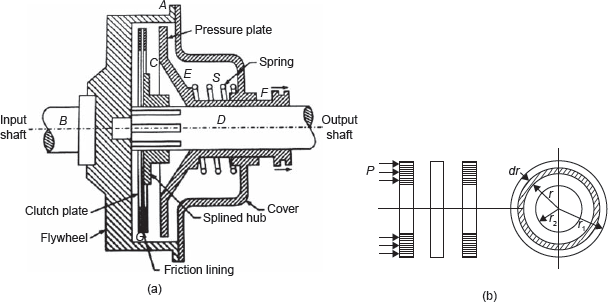
Figure 16.4 (a) Single Plate Clutch and (b) Friction Plate
When the withdrawal force is removed, the spring forces the pressure plate ‘E’ against the ring G. The friction between the contact surfaces of rings ‘G’ and plate ‘C’ transmits a torque on ‘D’ and driven shaft starts to rotate.
Let W = Axial load on the plate
T = Torque transmitted by clutch

Axial force on a small elemental ring of radius r and width dr, δW = P × 2πrdr
Frictional force,
Fr = μδW = μ × P × 2πrdr
Torque,
δT = Fr × r = μ × P × 2πrdr × r = μP2πr2dr
Now, there are two conditions:
- Uniform pressure for new clutch plate.
- Non-uniform wear for old or weared clutch plate.
Case I: Uniform Pressure
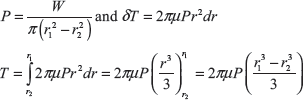
Putting the value of P, we get
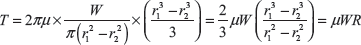
where R is mean radius and equals to ![]()
Case II: Uniform Wear
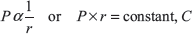
Normal force on the ring ![]()
Total force on the friction plate, ![]()
or
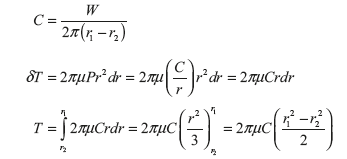
Putting the value of C, we get
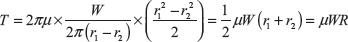
where R is mean radius and equals to ![]()
Example 16.1: A single plate disc clutch, both sides effective, has outer and inner radii as 250 mm and 150 mm. The maximum intensity of pressure at any point in the contact surface is not to exceed 0.1 N/mm2. If the coefficient of friction is 0.25, find the power transmitted by the clutch at a speed of 3,000 rpm (i) assuming uniform wear, and (ii) assuming uniform pressure.
Solution:
Given: r1 = 250 mm, r2 = 150 mm, P = 0.1 N/mm2, μ = 0.25, N = 3,000 rpm
- Considering uniform wear

- Considering uniform pressure

Example 16.2: A single plate disc clutch has both of its sides effective, transmits power at 250 rpm. The coefficient of friction is 0.25. The outer and inner radii of the friction plate are 100 mm and 40 mm, respectively. Assuming uniform wear of the clutch, the maximum pressure intensity is 0.1 N/mm2. If the moment of inertia of the rotating part of the clutch is 8 kg m2, calculate the time to attain the full speed by the machine and the energy lost during slipping of the clutch.
Assuming uniform pressure, find the intensity of pressure and compare the power transmitted with uniform wear to that with uniform pressure.
Solution:
Given: N = 250 rpm, μ = 0.25, r1 = 100 mm, r2 = 40 mm, P = 0.1 N/mm2, I = 8 kg m2
- Considering uniform wear

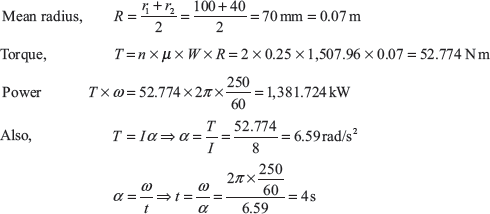
Energy loss during slipping period
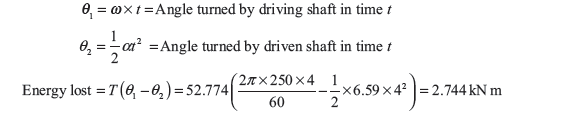
- With uniform pressure

Leave a Reply